Topper's Solved these Questions
PYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 3.4|12 VideosPYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 3.5|5 VideosPYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 3.2|6 VideosPROBABILITY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNEMENT 5.4|12 VideosQUADRATIC EQUATION
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise CHALLENGIN QUESTIONS|2 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-PYTHAGORAS THEOREM-Assignment 3.3
- Is (5,12,13) a Pythagorean triplet ? Give reason.
Text Solution
|
- In the figure, /QPR=90^(@), seg PM bot seg QR and Q-M-R, PM=10. QM=8, ...
Text Solution
|
- In DeltaABC, /ABC=90^(@), AB=12, BC=16 and seg BP is the median drawn ...
Text Solution
|
- Do sides 7cm, 24cm, 25cm form a right angled triangle? Give reason.
Text Solution
|
- Find the length of a diagonal of a rectangle having sides 11cm and 60c...
Text Solution
|
- Find the length of the hypotenuse of a right angeled triangle, if the ...
Text Solution
|
- Find the side of a square whose diagonal is 16sqrt(2)cm.
Text Solution
|
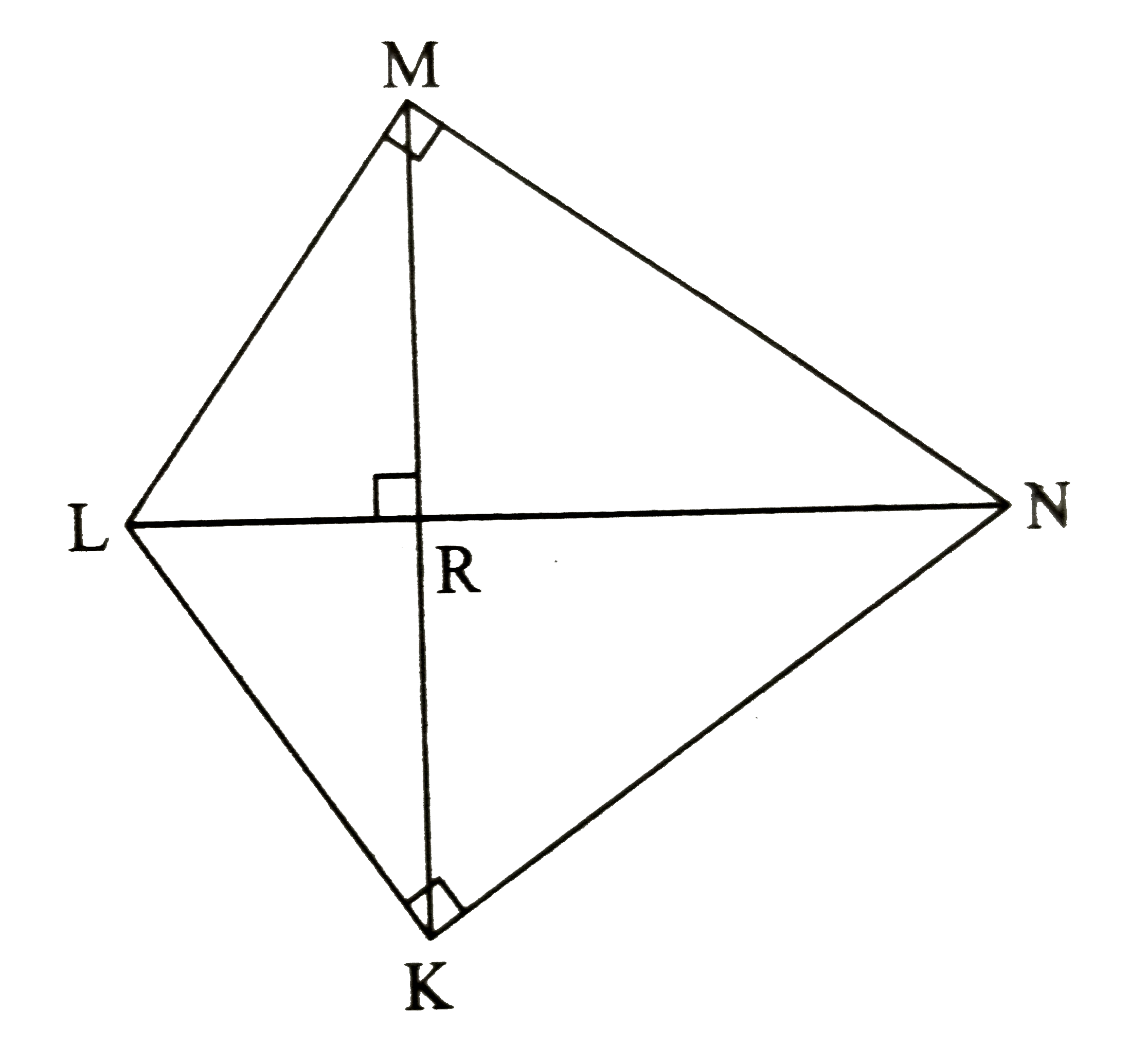
- In the figure, /LMN=/LKN=90^(@) seg MK bot seg LN. Complete the f...
Text Solution
|
- In order to prove, 'In a right angled triangle, the square of the hypo...
Text Solution
|