Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNMENT 4.1|10 VideosCIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNMENT 4.2|6 VideosCIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise 4.4 (1 mark each)|9 VideosCHALLENGING QUESTIONS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :|1 VideosCOORDINATE GEOMETRY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 6.5|13 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-CIRCLE-4.5 (1 mark each)
- In the figure, O is the centre of the circle . Seg AB is the diameter ...
Text Solution
|
- In Delta ABC, AB = AC. A circle passing through B touches side AC at ...
Text Solution
|
- In the figure, square ABCD is a parallalogram. It circumscribes the ci...
Text Solution
|
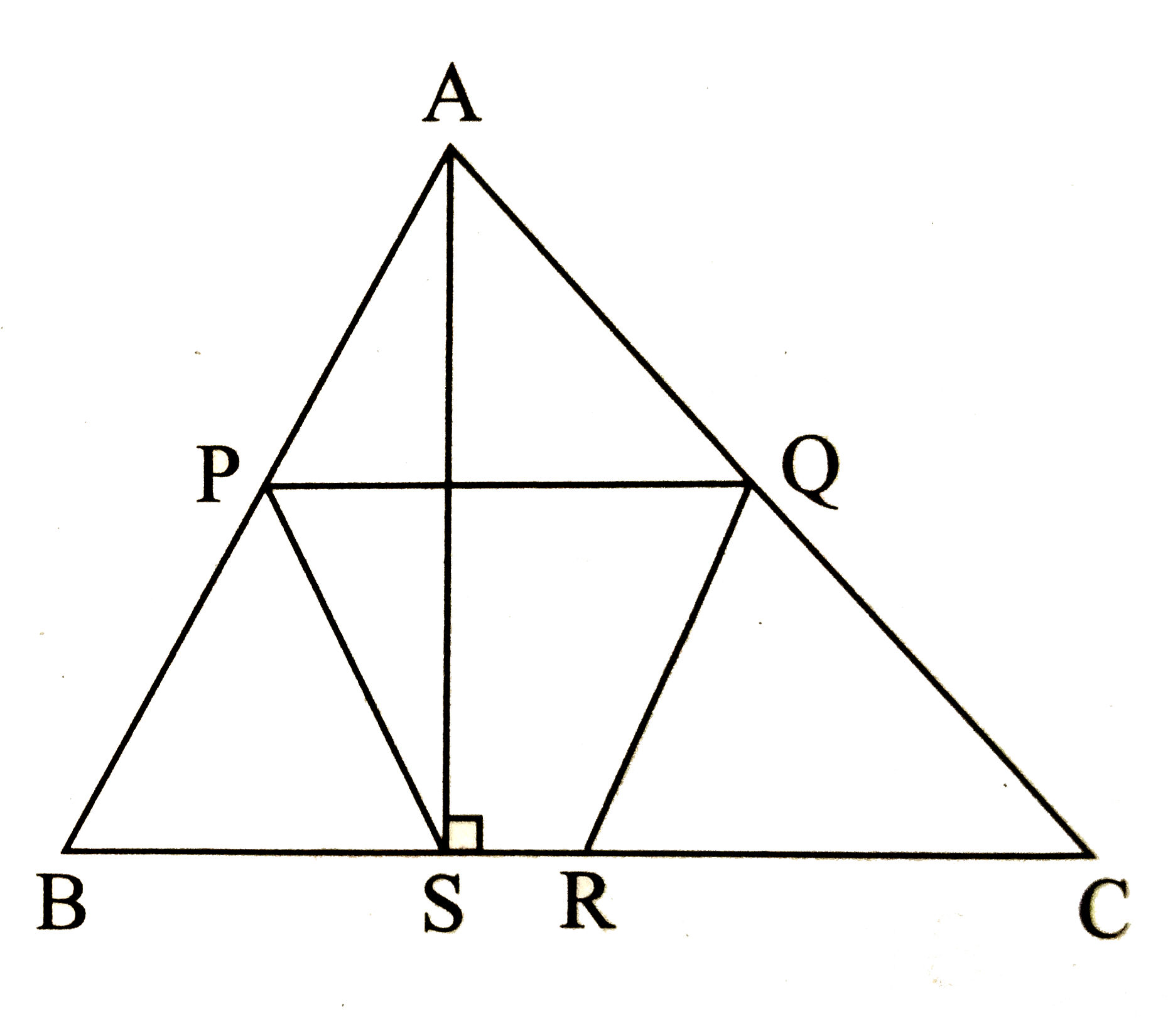
- In Delta ABC, P,Q and R are midpoints of sides AB,AC and BC respectiv...
Text Solution
|
- Delta ABC is inscribed in a circle with centre O and line AP is a tan...
Text Solution
|
- Let M be a point of contact of two internally touching circles. Let l...
Text Solution
|
- Two circles intersect each other at point P and Q. Secants drawn throu...
Text Solution
|