A tree 12 m high, is broken by the wind in such a way that its top touches the ground and makes an angles `60^(@)` with the gorund. At what height from the bottom the tree is broken by the wind?
Write your answer correct to the nearest m. `(sqrt(3) = 1.732)`

Explanation

In the figure AB represents the unbroken tree. C is the point where tree gets broken. The broken part BC takes the position CO. O is a point on the ground.
(`(1)/(2)` mark for figure and desription)
`AB = 12 m`
let `AC = x`
`AC + CB = AB`
`:. x + CB = 12`
`:. CB = (12 - x) m`

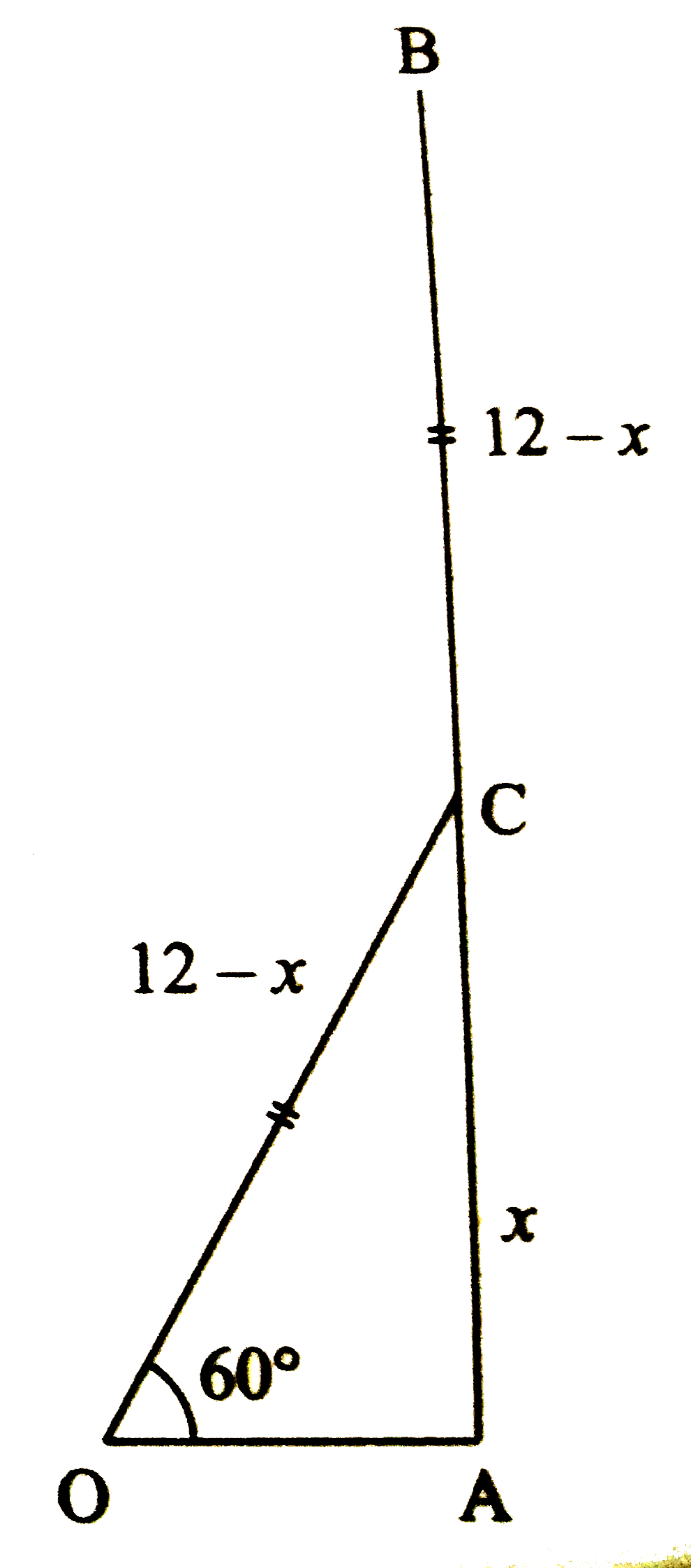
`:. CO = (12 - x)m`
In right angled `Delta CAO`,
`sin 60^(@) = (CA)/(CO)` ... (By definition)
`:. (sqrt(3))/(2) = (x)/(12 - x)`
`:. 12 sqrt(3) - sqrt(3) = 2x`
`:. 2 x + sqrt(3x) = 12 sqrt(3)`
`:. x (2 + sqrt(3)) = 12 sqrt(3)`
`:. x = (12 sqrt(3))/((2 + sqrt(3)))`
`:. x = (12 sqrt(3) (2 - sqrt(3)))/((2 + sqrt(3)) (2 - sqrt(3)))`
`:. x = (12 sqrt(3) (2 - sqrt(3)))/((2)^(2) - (sqrt(3))^(2))`
`x = (12 sqrt(3) (2 - sqrt(3)))/(4 - 3)`
`x :. (12 sqt(3) (2 - sqrt(3)))/(1)`
`:. x = 12 sqrt(3) (2 - sqrt(3))`
`:. x = 24 sqrt(3) - 36`
`:. x = 24 xx 1.732 - 36`
`:. x = 41.568 - 36`
`:. x = 5.568`
`:. x = 6 m` correct to the nearest m)