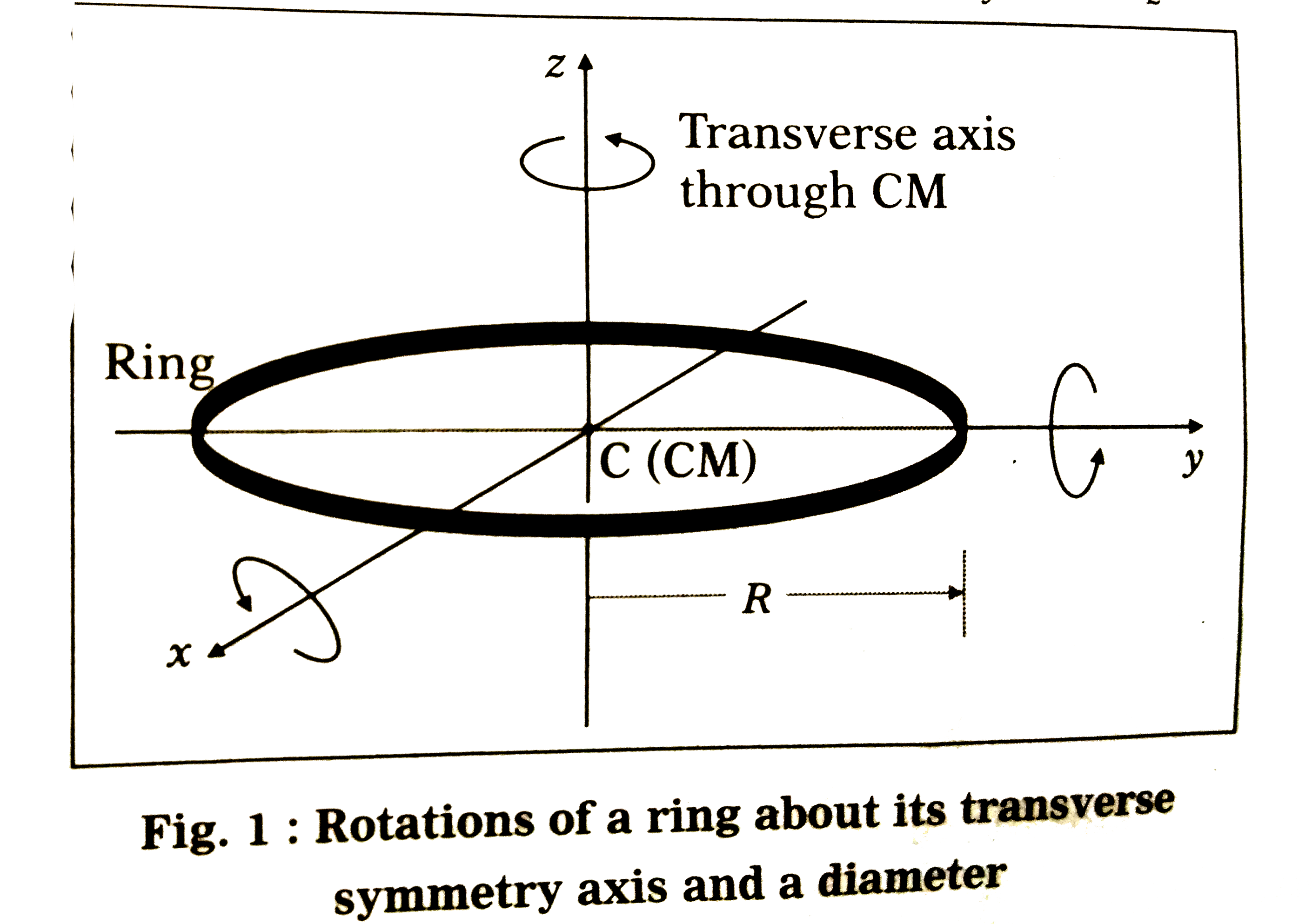
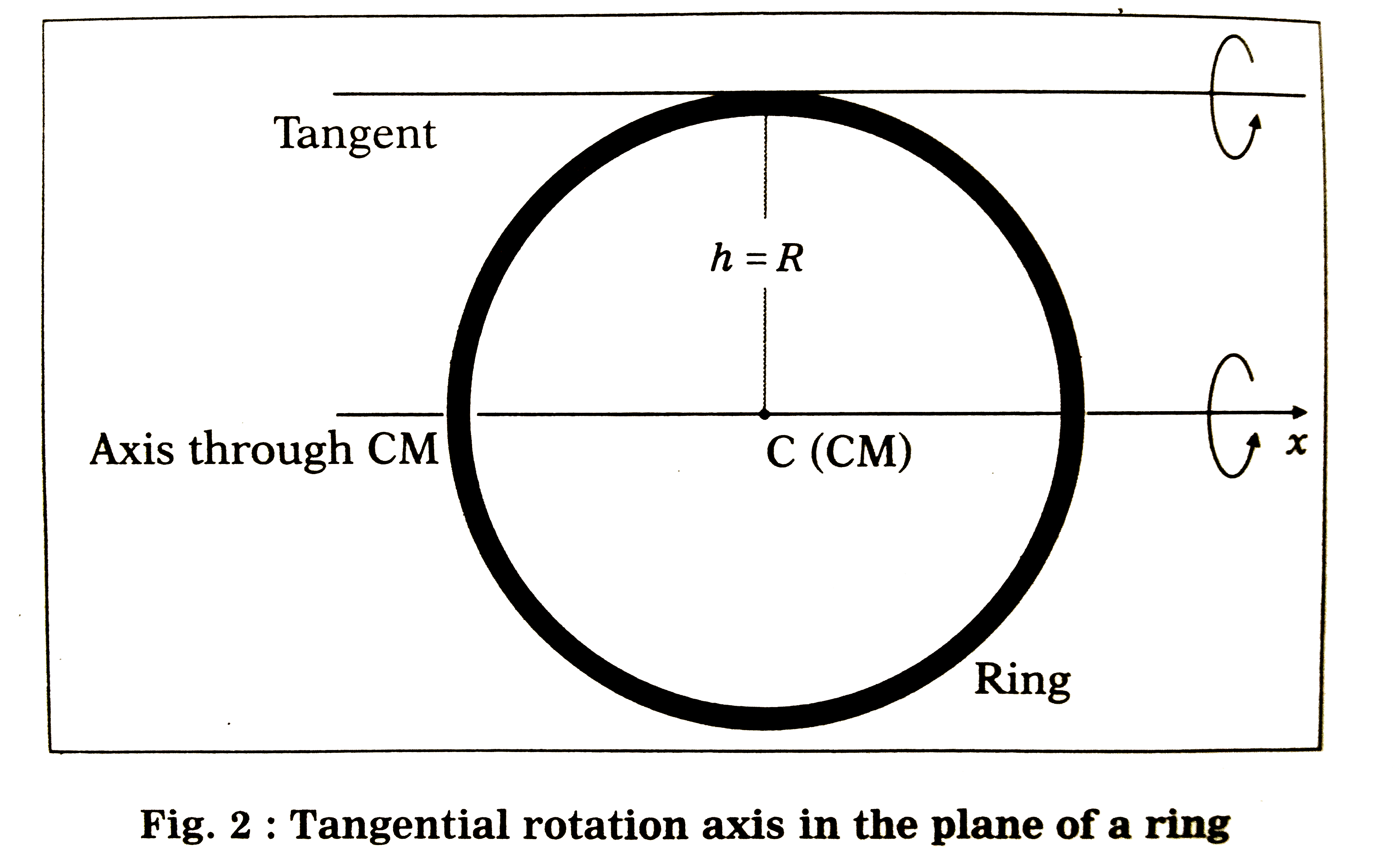
Text Solution
Verified by Experts
Topper's Solved these Questions
DERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Oscillations|5 VideosDERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Elasticity|2 VideosDERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Gravitation|7 VideosDEFINITIONS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise COMMUNICATION SYSTEMS|3 VideosDERIVATIONS-II
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignments|9 Videos
NAVNEET PUBLICATION - MAHARASHTRA BOARD-DERIVATIONS-I-Rotational Motion
- For a body rotating with constant angular velcoity, its kinetic energy...
Text Solution
|
- Torque acting on a rotating body
Text Solution
|
- State and prove theorem of parallel axes.
Text Solution
|
- State and prove theorem of perpendicular axes.
Text Solution
|
- The moment of inertia of a thin uniform rod about an axis passing thro...
Text Solution
|
- Moment of inertia of a disc about its own axis is I. Its moment of ine...
Text Solution
|
- State the expression for the moment of inertia of a thin uniform disc ...
Text Solution
|
- A solid sphere rolls on horizontal surface without slipping. What is t...
Text Solution
|
- Obtain an expression for total kinetic energy of a rolling body in ...
Text Solution
|
- If a rigid bady of radius 'R' starts from rest and rolls down an incli...
Text Solution
|
- A hollow cylinder and a solid cylinder are rolling without slipping do...
Text Solution
|
- Establish a relation between angular momentum and moment of inertia of...
Text Solution
|
- Obtain an expression for torque acting on a rotating body with constan...
Text Solution
|