लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
गतिमान आवेश और चुंबकत्व
PRABODH PUBLICATION|Exercise तथ्यात्मक प्रश्न|15 Videosगतिमान आवेश और चुंबकत्व
PRABODH PUBLICATION|Exercise अभ्यासार्थ प्रश्न (वस्तुनिष्ठ प्रश्न) I. बहुविकल्पीय प्रश्न|10 Videosगतिमान आवेश ओर चुम्बकत्व
PRABODH PUBLICATION|Exercise आंकिक प्रश्न|12 Videosचुम्बकत्व एवं पदार्थों के चुम्बकीय गुण
PRABODH PUBLICATION|Exercise मूल्य आधारित प्रश्न|6 Videos
PRABODH PUBLICATION-गतिमान आवेश और चुंबकत्व-मूल्य आधारित प्रश्न
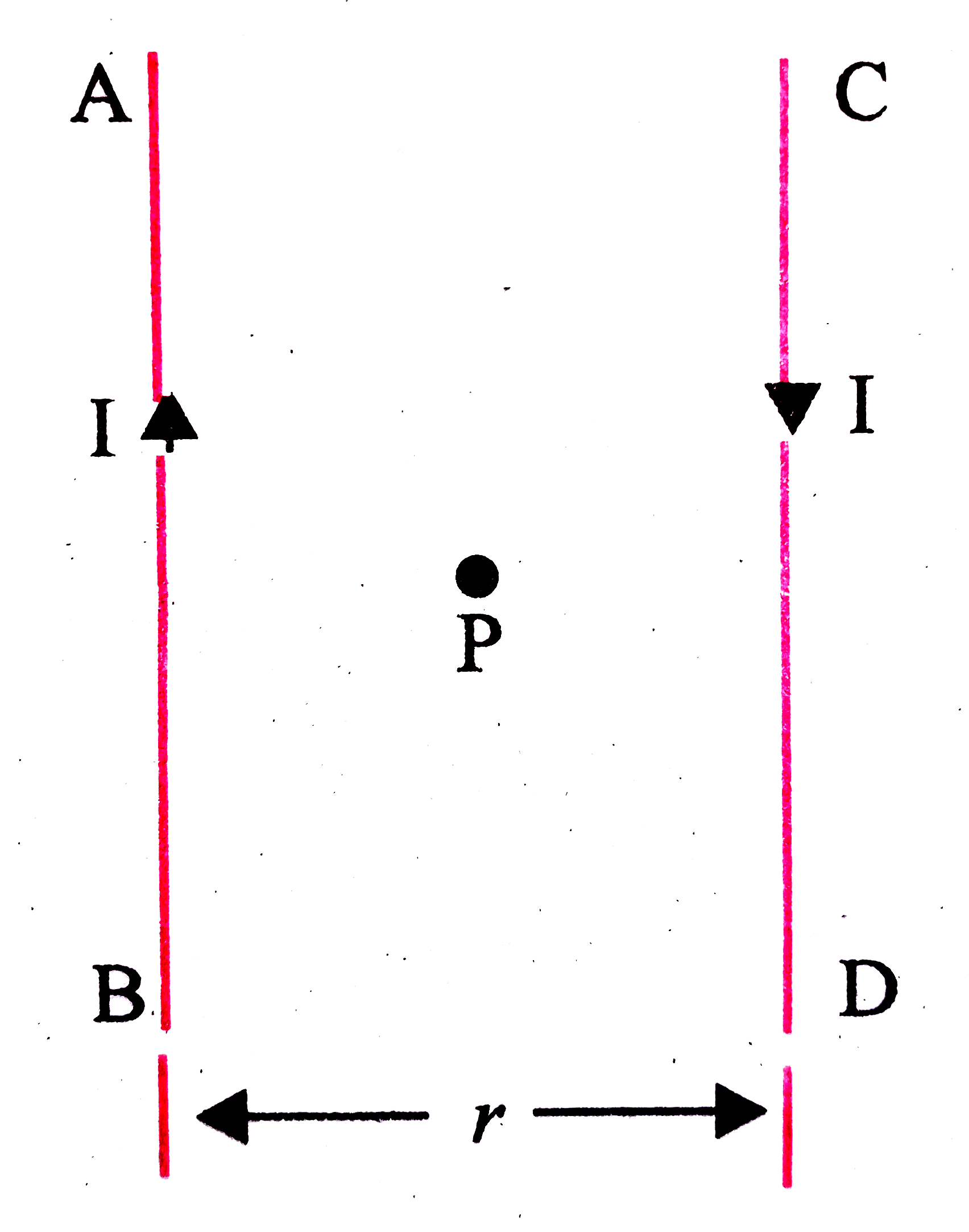
- अन्नत लम्बाई के दो समान्तर तारो में I धारा प्रवाहित हो रही है के बीच क...
Text Solution
|
- दो समांतर रेखीय धारावाही चालक में धारा समान दिशा में प्रवाहित ह...
Text Solution
|
- जब प्रतिरोध G का धारामापी, निम्न प्रतिरोध के शण्ट S के साथ संयोजित किय...
Text Solution
|
- एक आयताकार कुंडली जिसमे n फेरे है धारा I प्रवाहित हो रही है प्रत्येक क...
Text Solution
|