Home
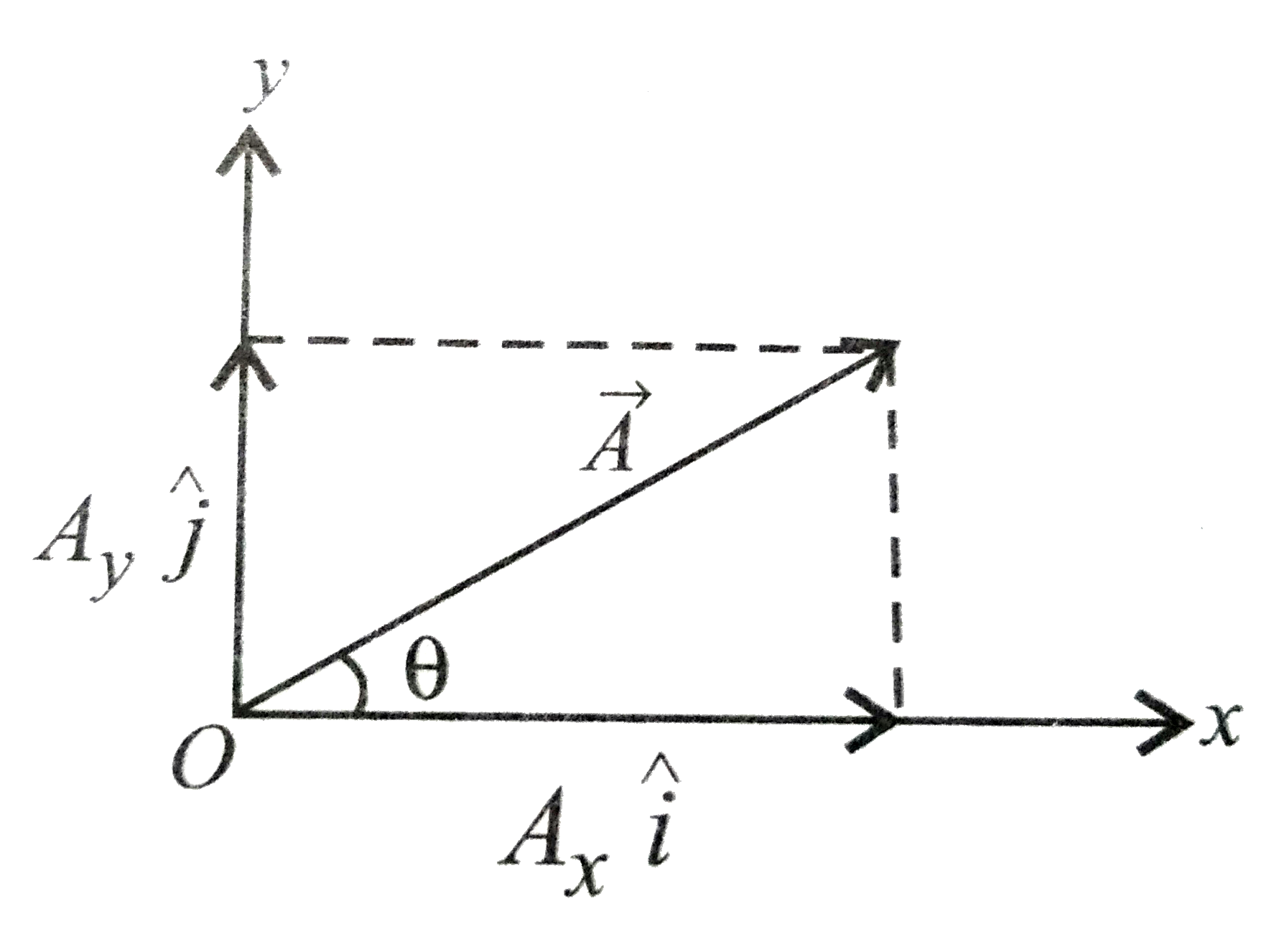
Class 11
PHYSICS
The magnitude of the x-component of vect...

The magnitude of the x-component of vector `vec(A)` is 3 and the magnitude of vector `vec(A)` is 5. What is the magnitude of the y-component of vector `vec(A)` ?

A

3

B

4

C

5

D

8

Text Solution

Verified by Experts

The correct Answer is:
B
`vecA = A_(x) hati + A_(y) hatj`
Also, `A = sqrt(A_(x)^(2) + A_(y)^(2))`
Here, `A = 5, A_(x) = 3`
`therefore 5 = sqrt((3)^(2) + A_(y)^(2))`
Squaring both sides, we get
`25 = 9 + A_(y)^(2) or A_(y) = 4`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PLANE

    NCERT FINGERTIPS|Exercise Vector Addition - Analytical Method|11 Videos

  • MOTION IN A PLANE

    NCERT FINGERTIPS|Exercise Motion In A Plane|10 Videos

  • MOTION IN A PLANE

    NCERT FINGERTIPS|Exercise Addition And Subtraction Of Vectors - Graphical Method|6 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    NCERT FINGERTIPS|Exercise Assertion And Reason|15 Videos

  • MOTION IN A STRAIGHT LINE

    NCERT FINGERTIPS|Exercise Assertion And Reason|15 Videos

Similar Questions

Explore conceptually related problems

If vec(A) is a vector of magnitude 3 units due east. What is the magnitude and direction of a vector -4vec(A) ?

The sum of three vectors shown in figure, is zero. (i) What is the magnitude of vector vec(OB) ? (ii) What is the magnitude of vector vec(OC) ?

If vec(A) is a vector of magnitudes 5 units due east. What is the magnitude and dirction of a vector -5vec(A) ?

vec A is a vector of magnitude 2.7 units due east . What is the magnitude and direction of vector 4 vecA ?

The sum of three vectors shown in Fig. 2 ( c) . 77. is zero . . (a) What is the magnitude of the vector vec (OB) ? (b) What is the magnitude of the vector vec (OC) ?

The x- component of a certain vector in x-y plane is 2 units and y- component is +2sqrt(3) units. What is the magnitude of the vector.

The x- component of a certain vertor is 2 units and y- component is + 2sqrt3 units. What is the magnitude of vector.

Write the magnitude of the vector vec(a) in terms of dot product.

The magnitude of x and y components of vec(A) are 7 and 6 respectively . Also , the magnitudes of x and y components of vec(A)+vec(B) are 11 and 9 respectively . Calculate the magnitude of vector vec(B)

The resultant of two vectors vec A and vec B is perpendicular to the vector vec A and its magnitude is equal to half the magnitude of vector vec B . What is the angle between vec A and vec B ?