A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-KINEMATICS-2-Exercise Comprehension
- A car is moving towards south with a speed of 20 m s^(-1). A motorcycl...
Text Solution
|
- A man can swim at a speed of 3 km h^-1 in still water. He wants to cro...
Text Solution
|
- A man can swim at a speed of 3 km h^-1 in still water. He wants to cro...
Text Solution
|
- To a stationary man, rain appears to be falling at his back at an angl...
Text Solution
|
- To a stationary man, rain appears to be falling at his back at an angl...
Text Solution
|
- From a tower of height 40 m, two bodies are simultaneously projected h...
Text Solution
|
- From a tower of height 40 m, two bodies are simultaneously projected h...
Text Solution
|
- From a tower of height 40 m, two bodies are simultaneously projected h...
Text Solution
|
- A ball is thrown from a point in level with velocity u and at a horizo...
Text Solution
|
- A ball is thrown from a point in level with velocity u and at a horizo...
Text Solution
|
- A 0.098-kg block slides down a frictionless track as shown in (Fig. )....
Text Solution
|
- A 0.098-kg block slides down a frictionless track as shown in (Fig. 5....
Text Solution
|
- A 0.098-kg block slides down a frictionless track as shown in (Fig. 5....
Text Solution
|
- A 0.098-kg block slides down a frictionless track as shown in (Fig. 5....
Text Solution
|
- A projectile is thrown with velocity v at an angle theta with the hori...
Text Solution
|
- A projectile is thrown with velocity v at an angle theta with the hori...
Text Solution
|
- A body is thrown at an angle theta0 with the horizontal such that it a...
Text Solution
|
- A particle is projected with a speed u at angle theta with the horizon...
Text Solution
|
- What is the radius of curvature of the parabola traced out by the proj...
Text Solution
|
- A particle is projected with a speed u at an angle theta to the horizo...
Text Solution
|
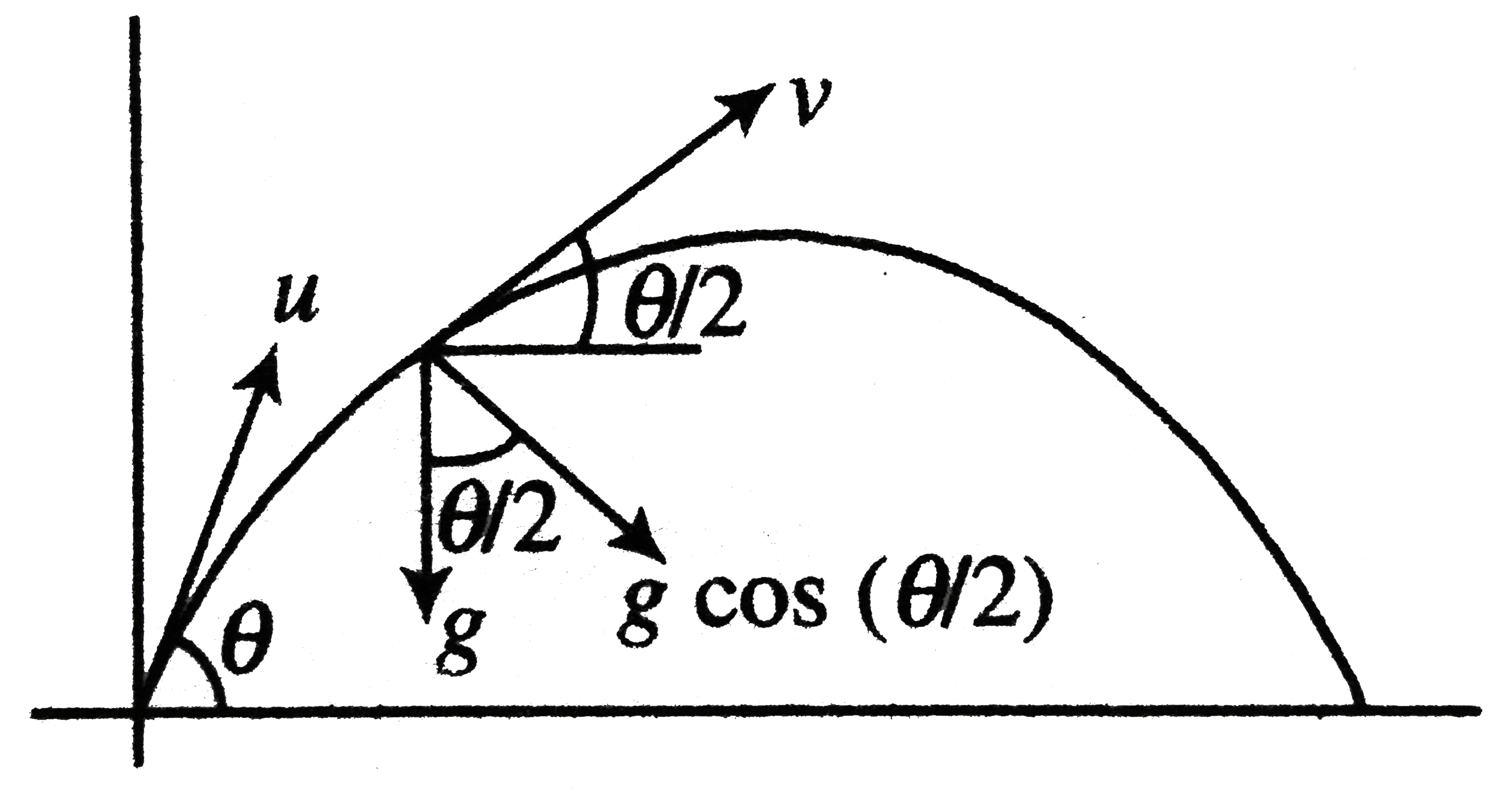 ,
,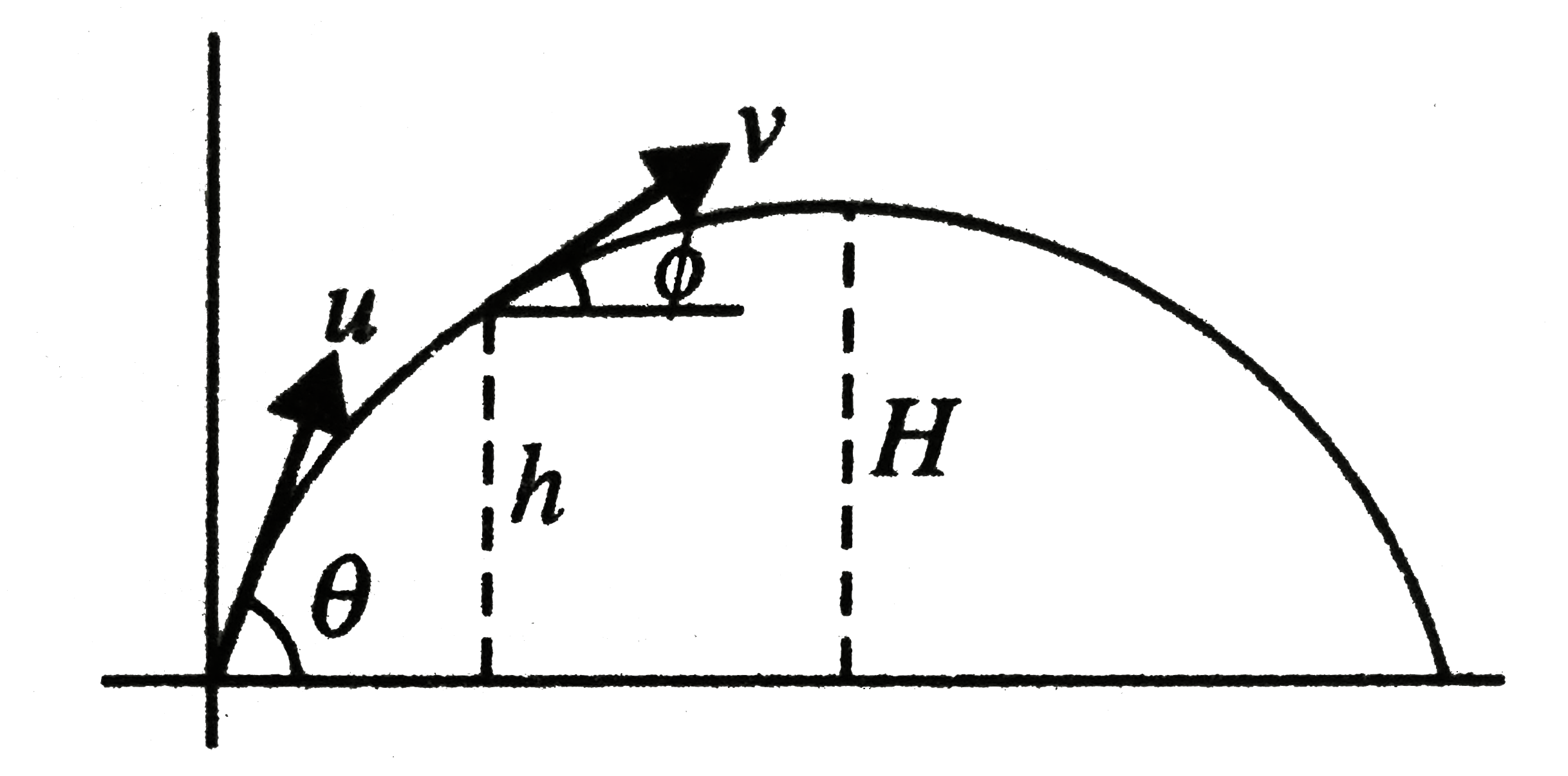 .
.