Two blocks are connected by a string, as shown in figure. They are released from rest. Show that after they have moved a distance L, their common speed is given by `v=sqrt(2(m_2-mum_1)gL//(m_1+m_2))`, in which `mu` is the coefficient of kinetic friction between the upper block and the surface. Assume that the pulley is massless and frictionless.

Explanation

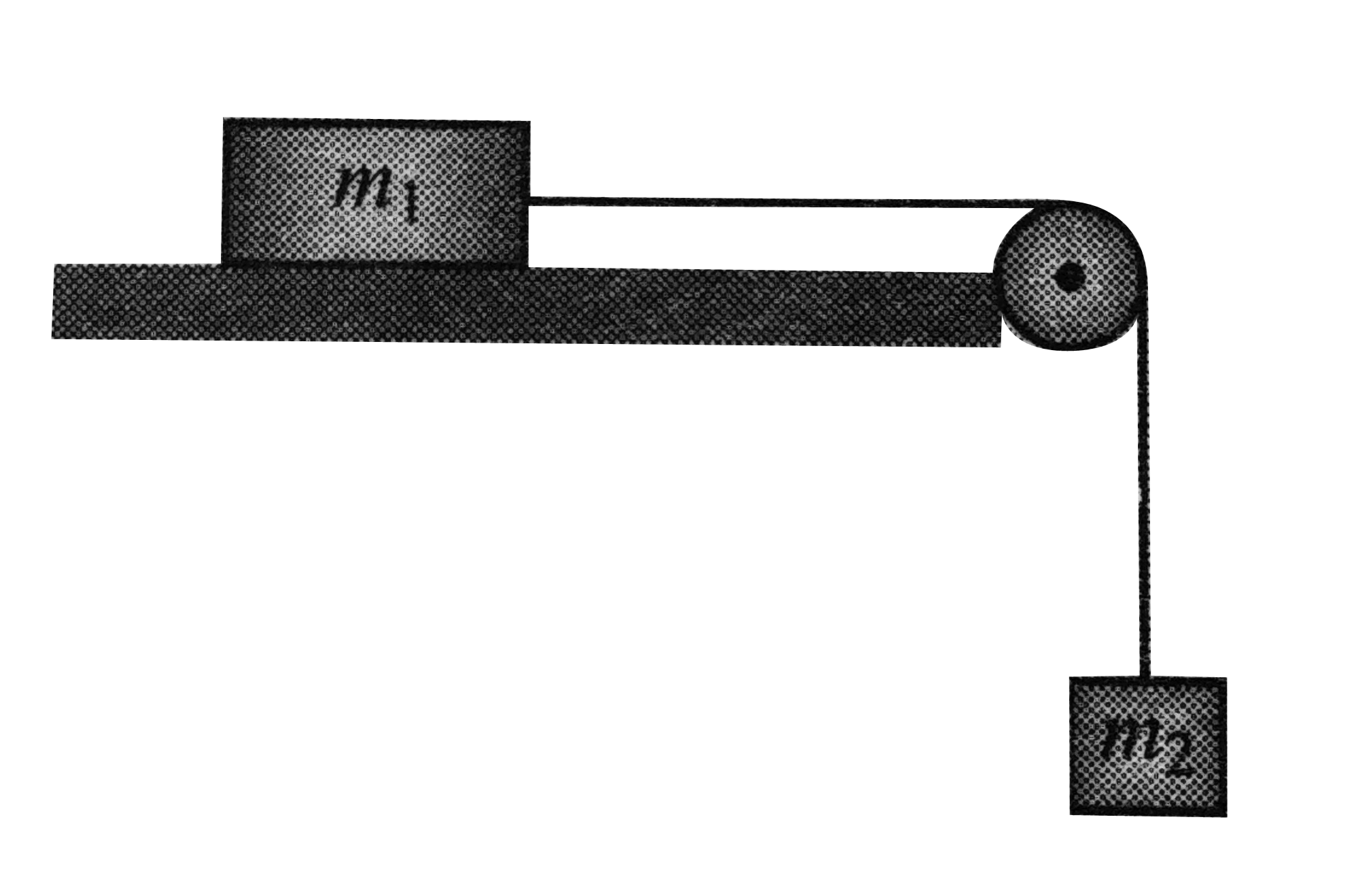
First we will solve the problem by the force method and then by the work-energy method. This will give you an opportunity to compare these two methods and sharpen your skills in selecting the method to be used for solving a prolem.
Force method: Let the acceleration of `m_1` be a horizontally towards right. The acceleration of `m_2` will be a vertically downwards (pulley constraint). Application of `sumvecF=mveca` to `m_1` and `m_2` (see the free body diagrams for `m_1` and `m_2` in figure shows

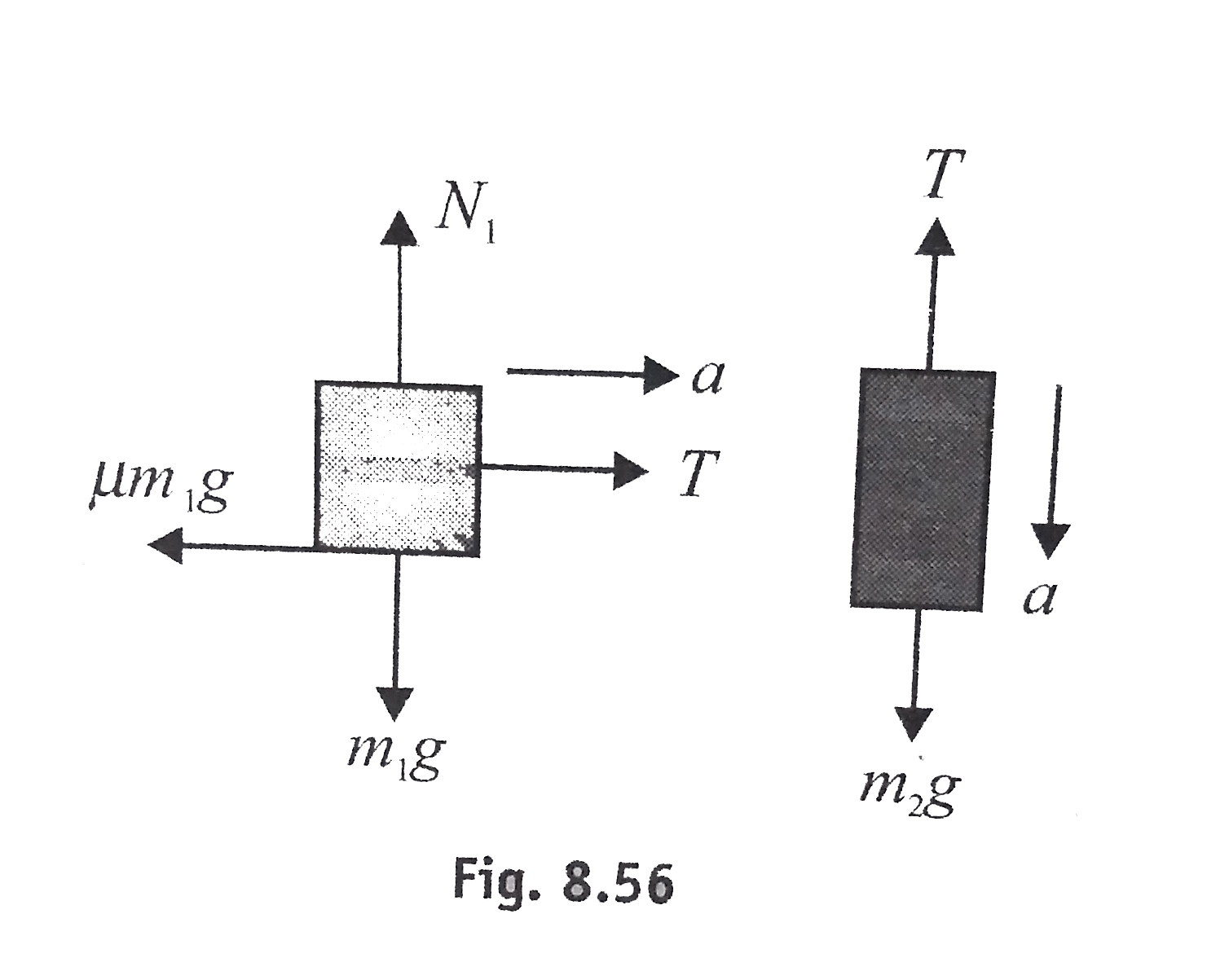
`T-mum_1g=m_1a` and `m_2g-T=m_2a`
Solving these equations for a, we get `a=((m_2-mum_1))/(m_1+m_2)g`
Using `s=ut+(1//2)at^2`, we find that the blocks take time.
`t=sqrt((2L(m_1+m_2))/((m_2-mum_1)g))`
to cover the ditance L, and from `v=u+at`, they will have the speed
`v=0+((m_2-mum_1)g)/(m_1+m_2)xxsqrt((2L(m_1+m_2)g)/((m_2-mum_1)g))`
`=sqrt((2Lg(m_2-mum_1))/(m_2+m_1))`
Work-energy method: The essence of the process in terms of energy considerations is that `m_2` loses potential energy of amount `m_2gL` while coming down by L, and the loss of potential energy of `m_2` appears partly in `m_1` and `m_2` in the form of kinetic energy and is partly used up as as work done against friction.
`m_2gL=1/2(m_1+m_2)v^2+mum_1gL`
`implies(m_2-mum_1)gL=1/2(m_1+m_2)v^2`
`impliesv=sqrt((2(m_2-mum_1)gL)/(m_1+m_2))`