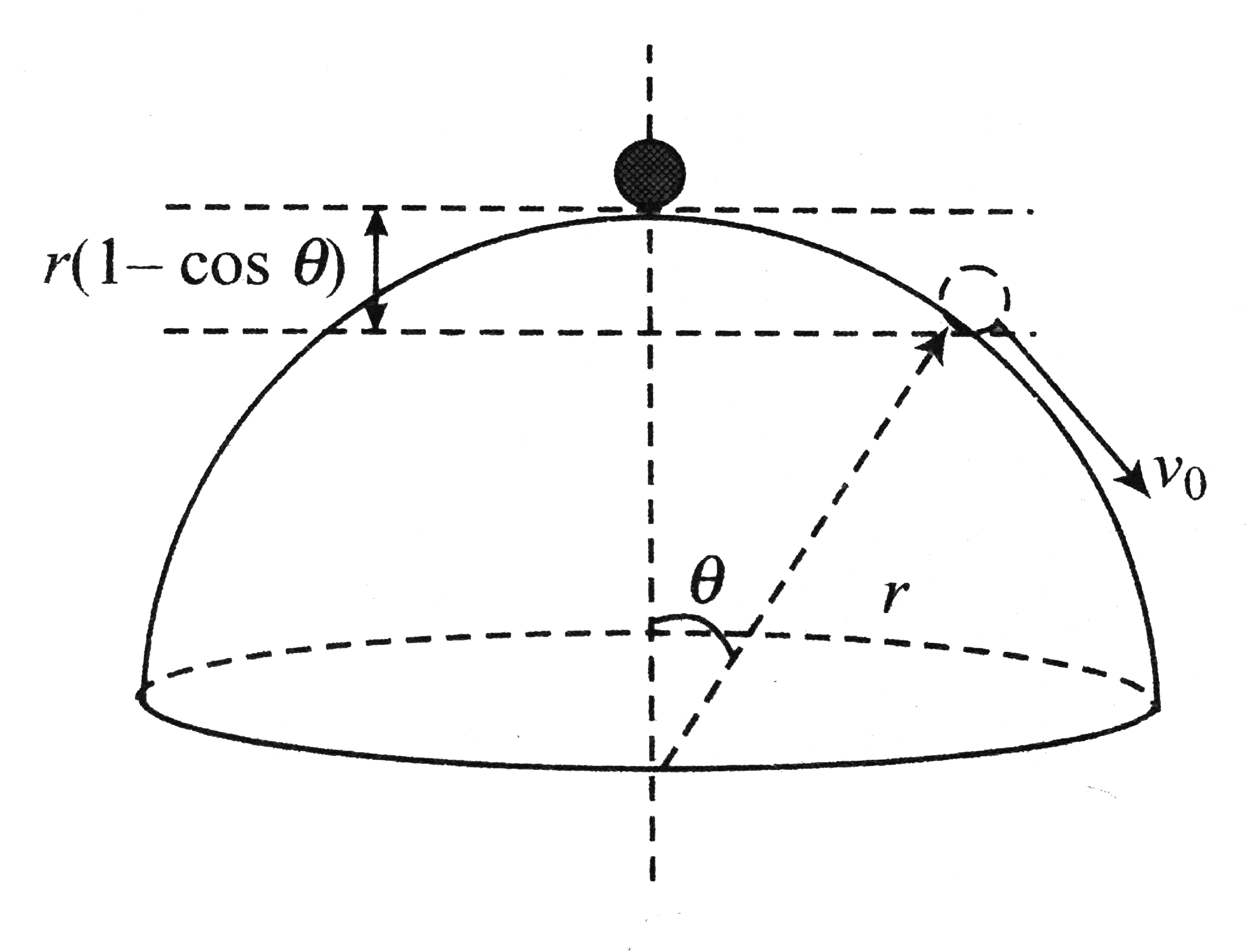
a. As the particle is moving down w.r.t. earth, hence, the potential energy of the particle will decrease.
Change in potential energy,
`DeltaU=U_(theta)-U_0=-mgr(1-costheta)` (i)
b. The force acting on the point mass are a conservative force `mg` and a non-conservative force N. Here `W_N=0` because all along the motion from the `theta=0` to `theta=theta`, the velocity of the mass is perpendicular to N. Consequently, the mechanical energy of m remains constant.
`DeltaK+DeltaU=0`
`(K_theta-K_0)+DeltaU=0`
`K_theta=K_0-DeltaU`
`=0-[-mgr(1-costheta)]`
`=mgr(1-costheta)` (ii)
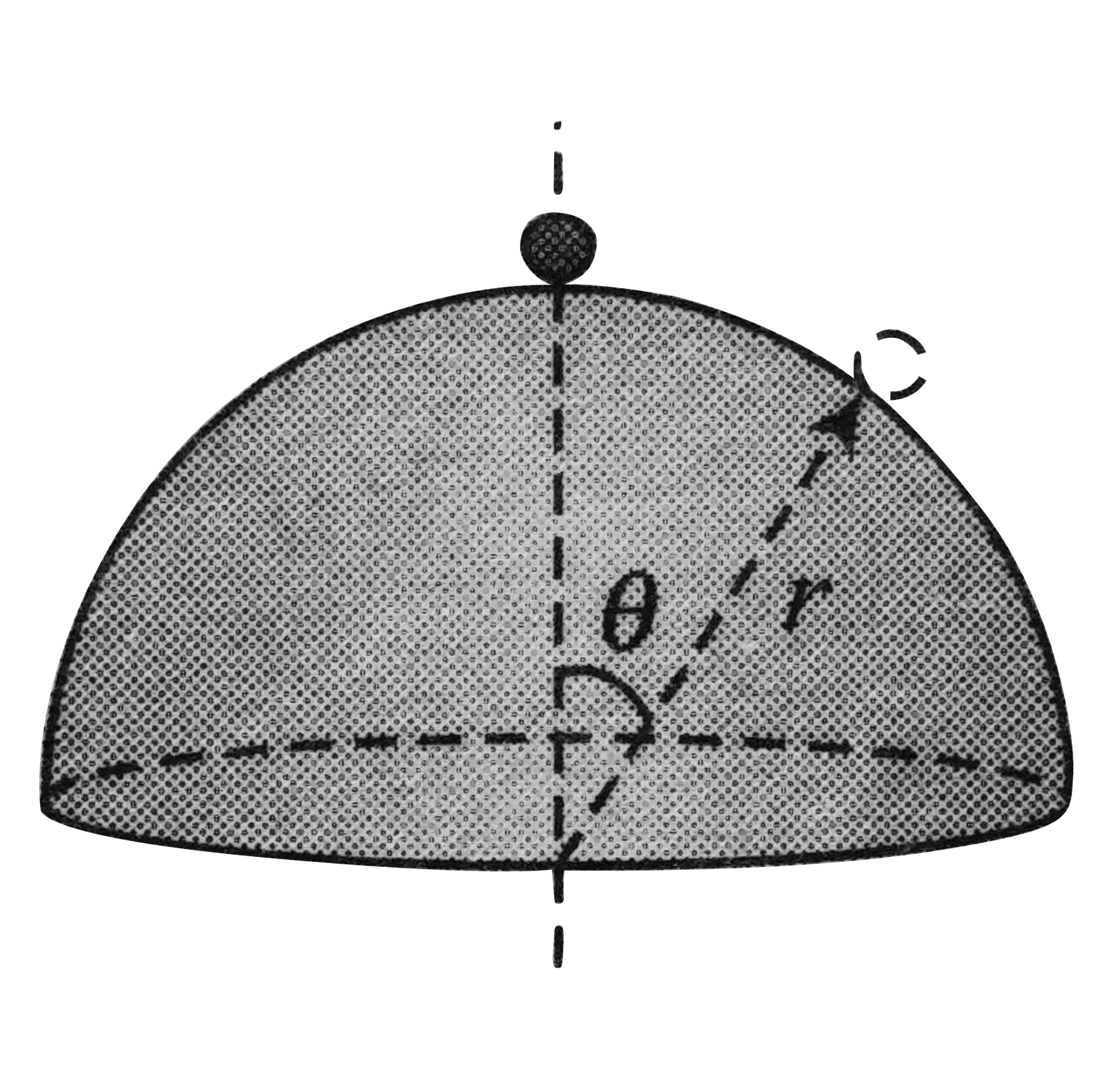
c. Figure shows the free body diagram of m at `theta`. The radial acceleration of m at this position
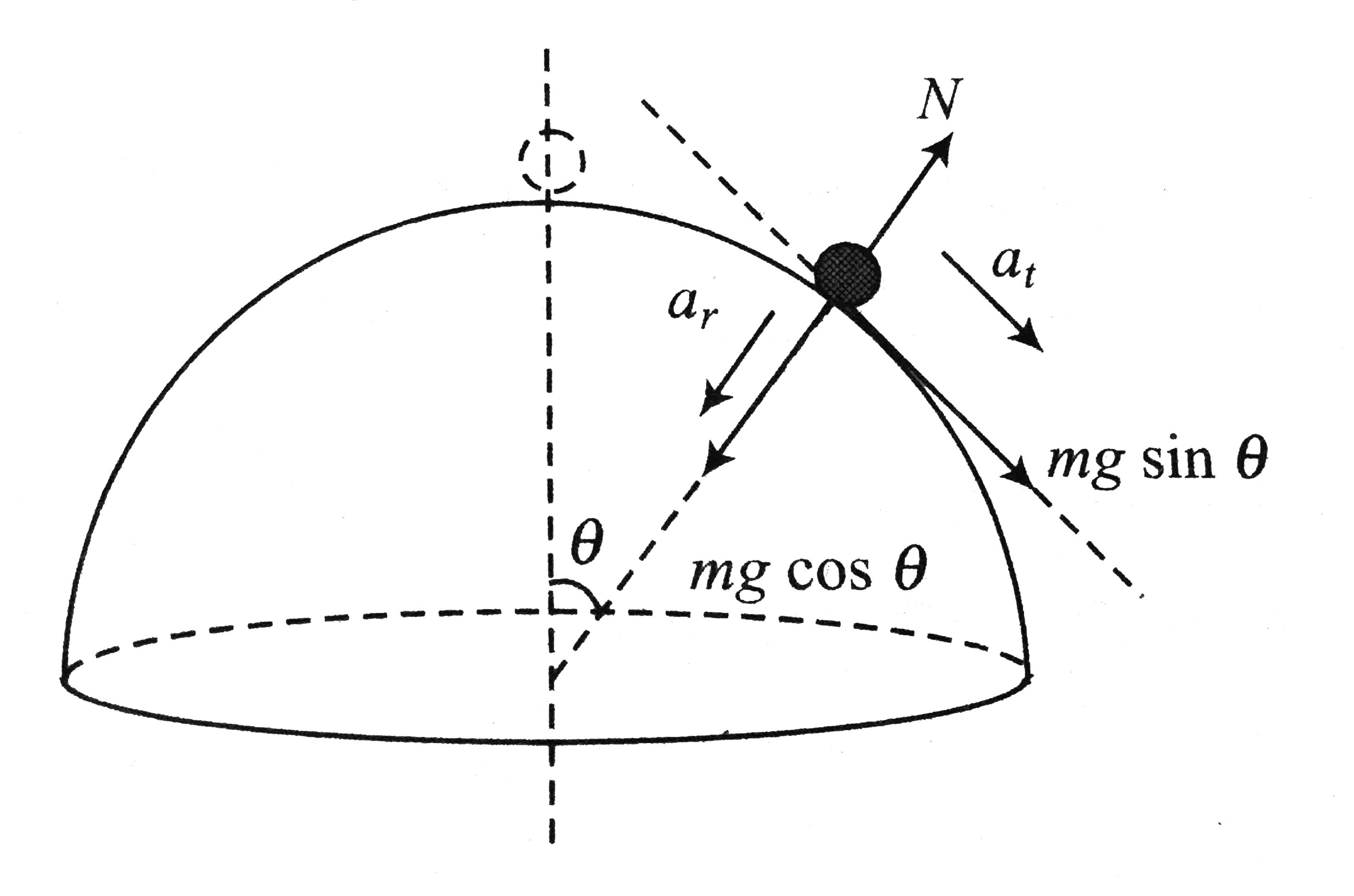
`a_r=(v_theta^2)/(r)`.
`=(2gr(1-costheta))/(r)=a_r=2g(1-costheta)`
Force equation for m in the tangential direction is
`mg sin theta=ma_tauimpliesa_t=g sin theta`
d. Angle at which the mass flies off the sphere:
Force equation in the radial direction,
`mgcostheta-N=(mv^2)/(r)` (iii)
As the masss slide, down the sphere, its speed increases. So the right hand slide of the equation (iii), `mv^2//r`, increases with increasing `theta`. Also `mg cos theta` decreases as `theta` increases,
(for `0ltthetaltpi//2`, `cos theta` decreases as `theta` increases).
N must decrease with increasing `theta`. The angle at which `Nrarr0`, the mass loses contact with the sphere, it flies off it. Let this happen when `thetararralpha`. At `thetararralpha`. `Nrarr0`, `vrarrv_alpha`.
Under this limiting condition, equation (iii) reduces to
`impliesmg cos alpha-0=(mv_alpha^2)/(r)` (iv)
Conservation of mechanical energy between `theta=0` and `theta=alpha` gives, `DeltaK+DeltaU=0`
`implies[1/2mv_alpha^2-0]+[-mgr(1-cosalpha)]=0` (v)
From equation (iv) and (v),
`implies(((mv_alpha^2)/(r)))/((1/2mv_alpha^2))=(mgcosalpha)/(mgr(1-cosalpha))`
`implies((1/r))/((1/2))=(cosalpha)/(r(1-cosalpha))`
`implies2=(cosalpha)/(1-cosalpha)`
`implies2-2cos alpha=cos alpha`
`cos alpha=2/3impliesalpha=cos^-1(2/3)`
e. If friction is present, the speed at `theta=alpha` will be less than `v_alpha` defined in part (d), and `mg=cosalpha=mv^2//r` will not be satisfied. In fact, then `mgcosalphagtmv^2//r` as `vltv_alpha` and, cosequently, Newton's second law of motion will demand that.
`N=mg cos alpha-(mv^2)/(r)impliesNgt0`
For N to vanish, both `theta` and v must increase a little more.
Therefore with friction present, the mass fly off the sphere at a greater angle than in part(d).