A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-WORK, POWER & ENERGY-Single Correct
- A particle of mass m moves with a variable velocity v, which changes w...
Text Solution
|
- A particle of mass m moves along a circular path of radius r with a ce...
Text Solution
|
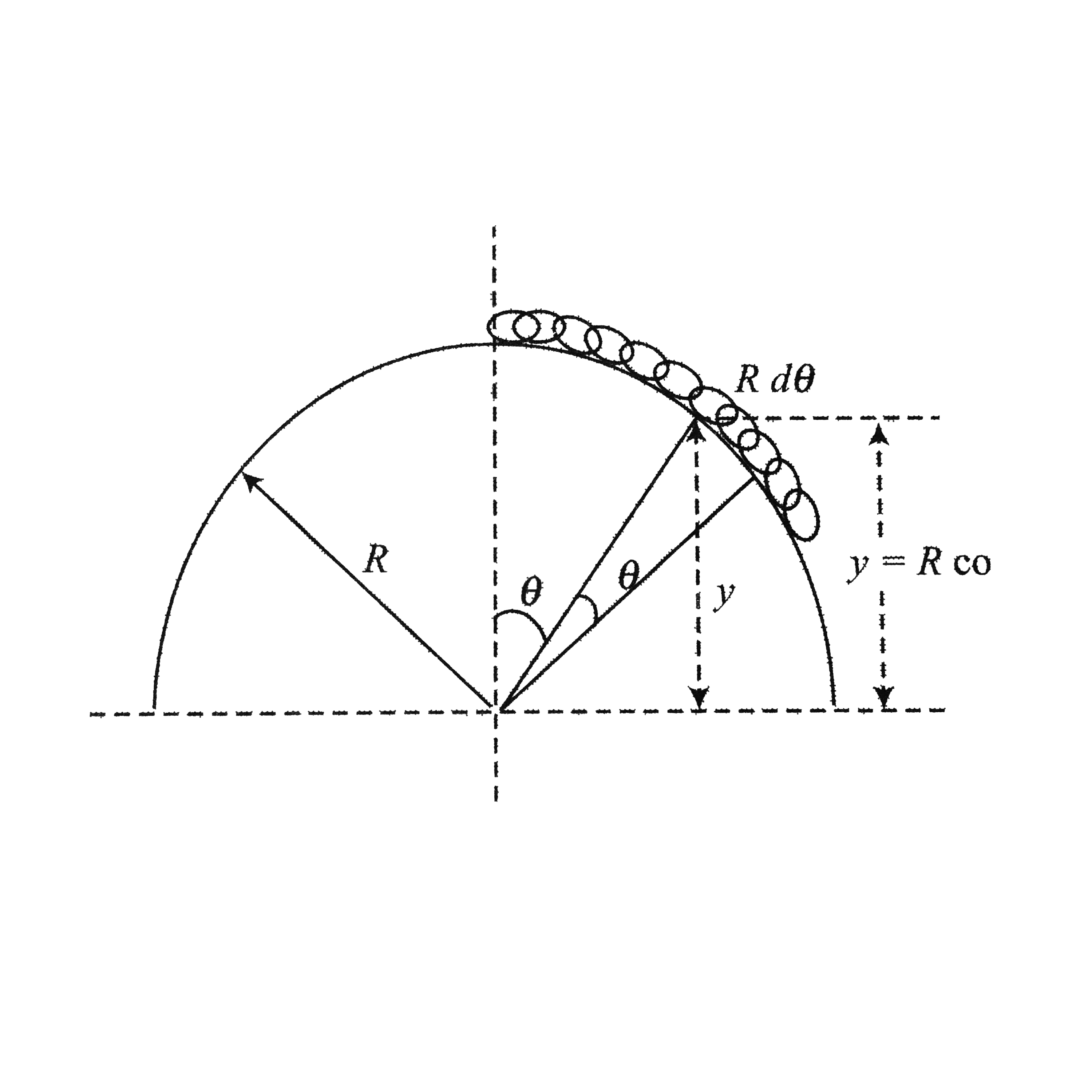
- A chain of length l and mass m lies of the surface of a smooth hemisph...
Text Solution
|
- Two discs, each having mass m, are attached rigidly to the ends of a v...
Text Solution
|
- Two ends A and B of a smooth chain of mass m and length l are situated...
Text Solution
|
- A block m is kept stationary on the surface of an accelerating cage as...
Text Solution
|
- A man places a chain (of mass m and length l) on a table slowly. Initi...
Text Solution
|
- The potential energy of a particle of mass m free to move along the x-...
Text Solution
|
- The blocks A and B shown in figure have masses MA=5kg and MB=4kg. The ...
Text Solution
|
- A collar B of mass 2kg is constrained to move along a horizontal smoot...
Text Solution
|
- A block attached to a spring, pulled by a constant horizontal force, i...
Text Solution
|
- A particle is projected along a horizontal field whose coefficient of ...
Text Solution
|
- Two identical blocks A and B are placed on two inclined planes as show...
Text Solution
|
- A block of mass m is being pulled up a rough incline by an agent deliv...
Text Solution
|
- The given plot shows the variation of U, the potential energy of inter...
Text Solution
|
- One end of an unstretched vertical spring is attached to the ceiling a...
Text Solution
|
- The potential energy function associated with the force vecF=4xyhati+2...
Text Solution
|
- The potential energy for a force filed vecF is given by U(x,y)=cos(x+y...
Text Solution
|
- A particle is projected with a velocity u making an angle theta with t...
Text Solution
|
- A block of mass m is attached with a massless spring of force constant...
Text Solution
|