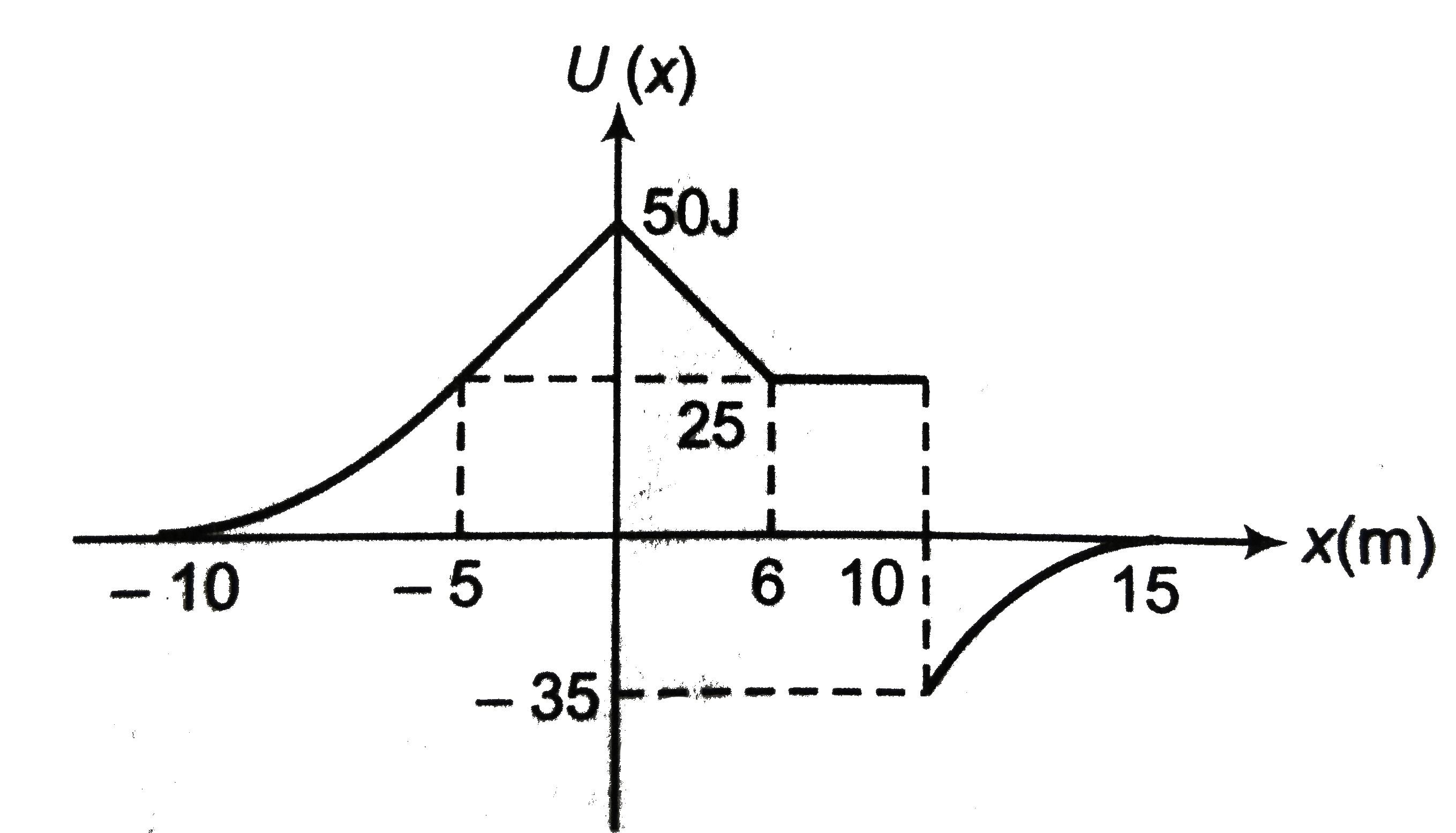
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-WORK, POWER & ENERGY-Linked Comprehension
- A srping lies along the x-axis attached to a wall at one end and a blo...
Text Solution
|
- A srping lies along the x-axis attached to a wall at one end and a blo...
Text Solution
|
- A small ball is given some velocity at point A towards right so that i...
Text Solution
|
- A small ball is given some velocity at point A towards right so that i...
Text Solution
|
- A small ball is given some velocity at point A towards right so that i...
Text Solution
|
- The figure shows the variation of potential energy of a particle as a ...
Text Solution
|
- Figure shows the variation of potential energy of a particle as a func...
Text Solution
|
- Figure shows the variation of potential energy of a particle as a func...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- Force acting on a particle moving in the x-y plane is vecF=(y^2hati+xh...
Text Solution
|
- A small block of mass m is pushed on a smooth track from position A wi...
Text Solution
|
- A small block of mass m is pushed on a smooth track from position A wi...
Text Solution
|
- A small block of mass m is pushed on a smooth track from position A wi...
Text Solution
|
- A force F=50N is applied at one end of a string, the other end of whic...
Text Solution
|
- A force F=50N is applied at one end of a string, the other end of whic...
Text Solution
|
- A force F=50N is applied at one end of a string, the other end of whic...
Text Solution
|