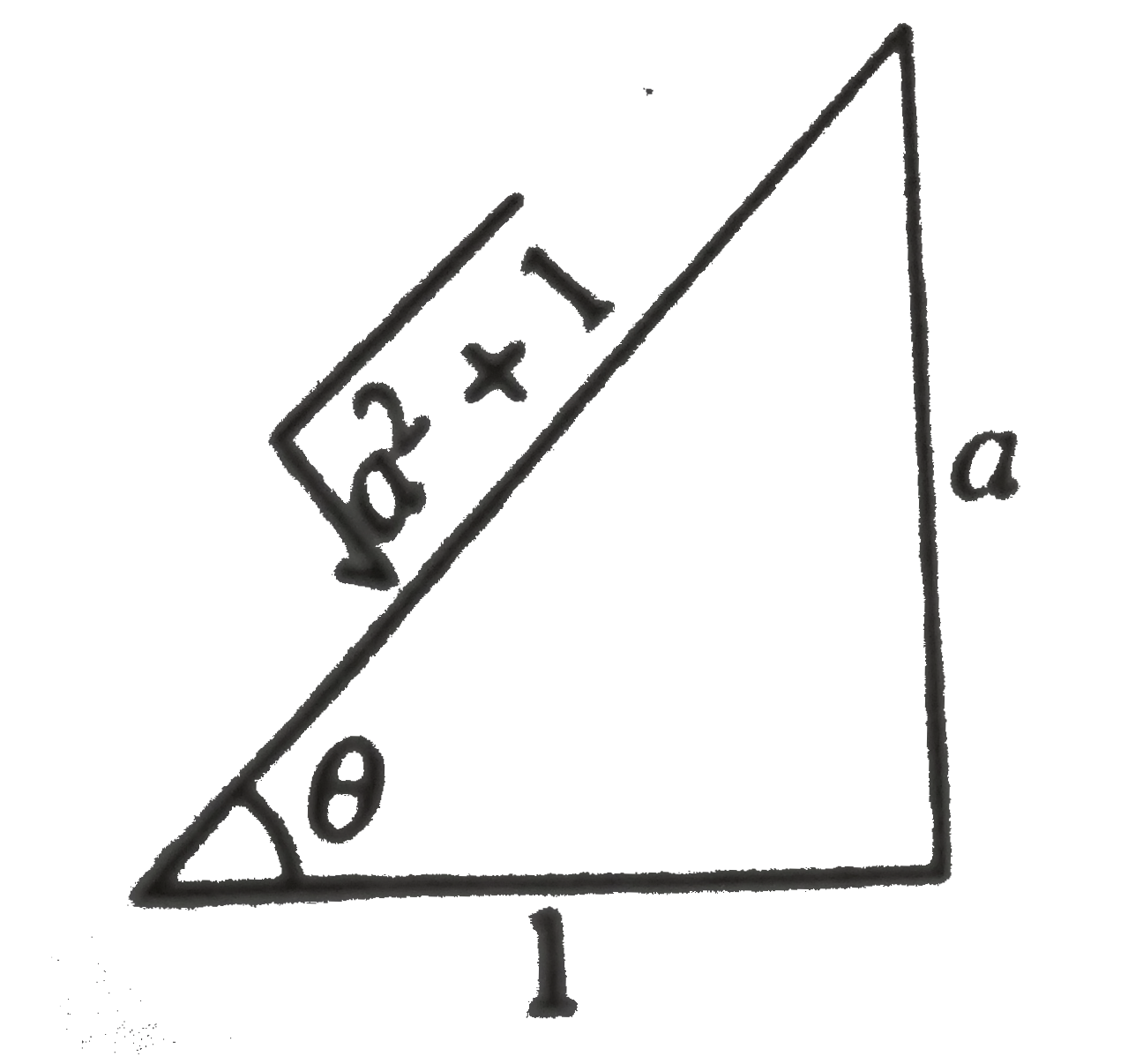
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise True or False|2 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Integer Type|17 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Multiple Correct Answer Type|9 VideosMISCELLANEOUS VOLUME 2
CENGAGE PHYSICS|Exercise INTEGER_TYPE|10 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-MISCELLANEOUS KINEMATICS-Fill in the blanks
- A particle moves in a circle of radius R. In half the period of revolu...
Text Solution
|
- Four person K,L,M and N are initally at the corners of a square of sid...
Text Solution
|
- Spotlight S rotates in a horizontal plane with constant angular veloc...
Text Solution
|
- The trajectory of a projectile in a vertical plane is y=ax-bx^(2), whe...
Text Solution
|