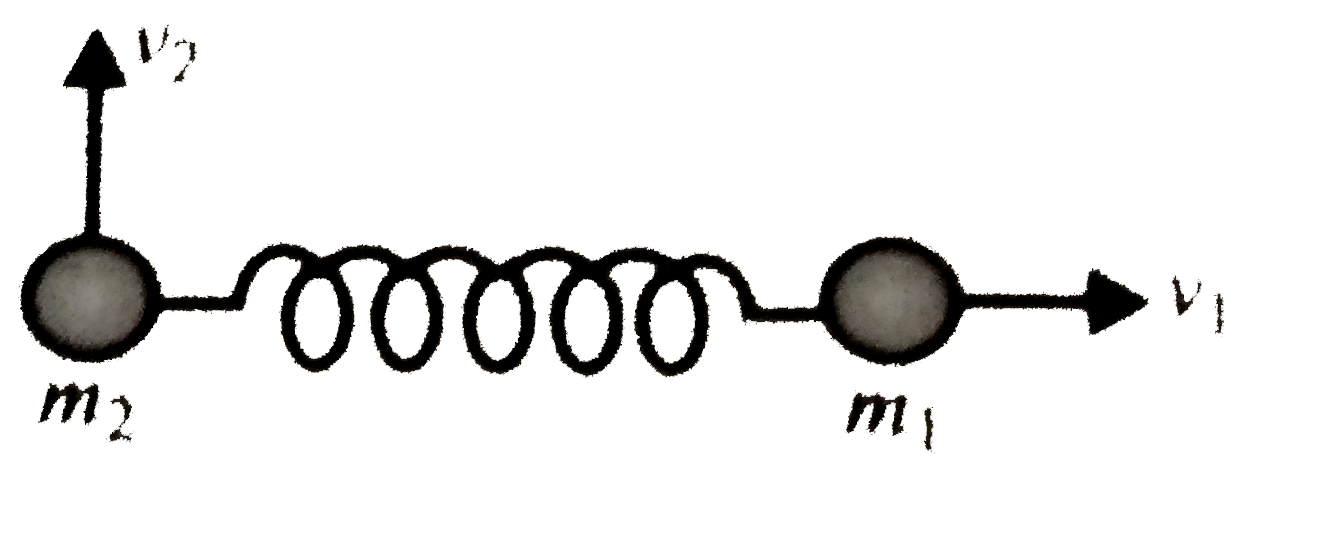
Two small discs of masses `m_(1)` and `m_(2)` are connected by a weightless spring resting on a smooth horizontal plance. The discs are set in motion with initial velocities `v_(1) and v_(2)` whose directions are mutually perpendicular and in the same horizontal plane. Find the total energy `E` of hte system with reference to the frame fixed to the centre of mass.

Explanation

Let `vecv_(cm)` be the velocity of the centre of mass. Velcoity of `m_(1)` relative to thecentre of mas is `(vecv_(1)-vecv_(cm))` and that of `m_(2)` relative to the centre of mass is `(vecv_(2)-vecv_(1))`
Velocity of centre of mass `vecv_(cm)=(m_(1)vecv_(1)m_(2)vecv_(2))/(m_(1)+m_(2))`
`(vecv_(1)-vecv_(cm))=m_(2)/(m_(1)+m_(2))(vecv_(1)-vecv_(2))`
Hence `|vecv_(1)-vecv_(cm)|=m_(2)/(m_(1)+m_(2)(v_(1)^(2)+v_(2)^(2))^(1//2)`
and `vecv_(2)-vecv_(cm)=m_(1)/(m_(1)+m_(2))(vecv_(2)-vecv_(1))`
Hence `|vecv_(2)-vecv_(cm)|=m_(1)/(m_(1)+m_(2))(v_(1)^(2)+v_(2)^(2))^(1//2)`
total energy with respect to the centre of mass,
`E=1/2m_(1)|vecv_(1)-vecv_(cm)|^(2)1/2m_(1)|vecv_(2)-vecv_(cm)|^(2)`
`=1/2((m_(1)m_(2))/(m_(1)+m_(2)))(v_(1)^(2)+v_(2)^(2))`
where `mu=(m_(1)m_(2))/(m_(1)+m_(2))` is called reduced mass.