A smooth wedge of mass `M` rests on a smooth horizontal surface. A block of mass `m` is projected from its lowermost point with velocity `v_(0)`. What is the maximum height reached by the block?
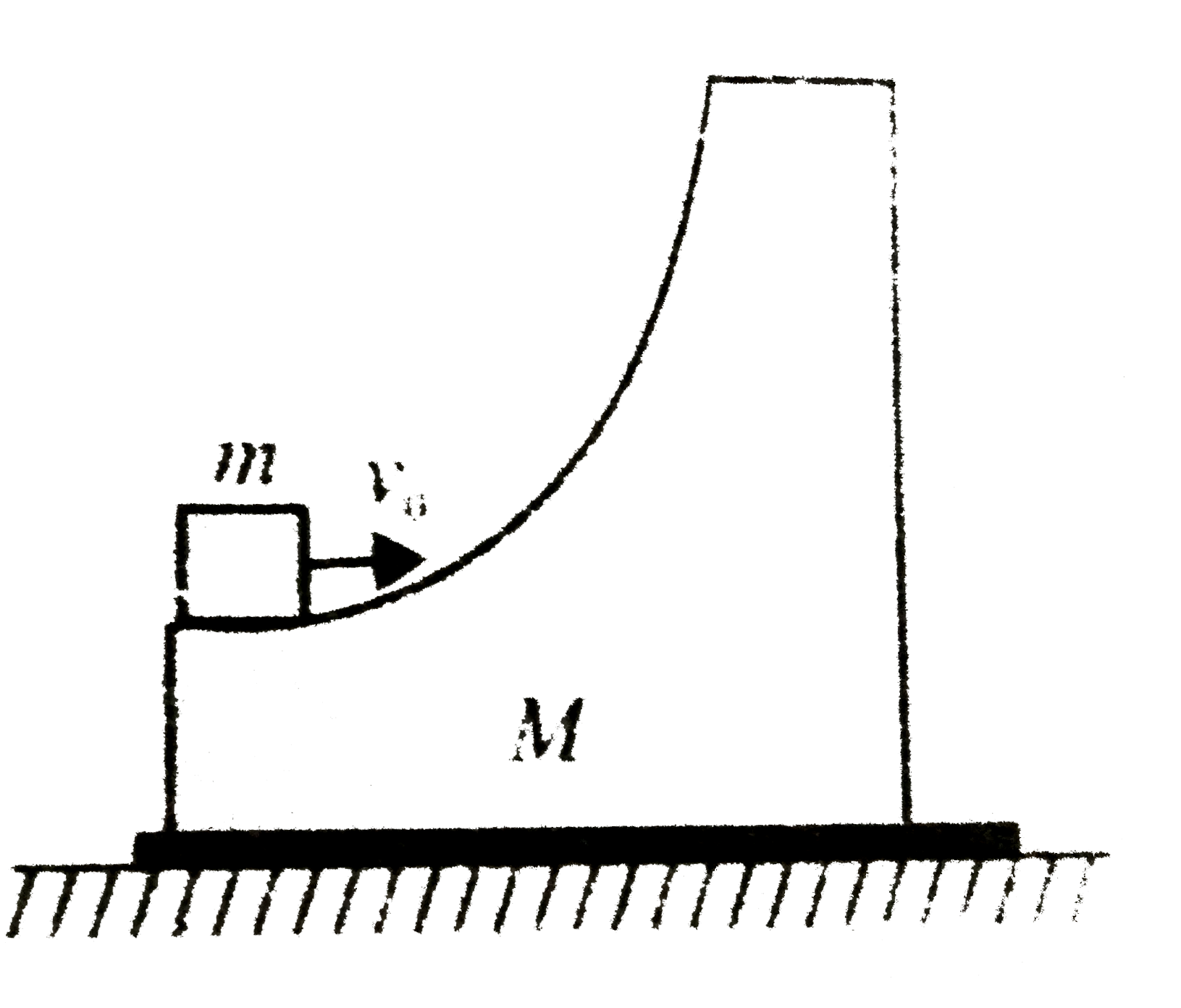
A smooth wedge of mass `M` rests on a smooth horizontal surface. A block of mass `m` is projected from its lowermost point with velocity `v_(0)`. What is the maximum height reached by the block?


Text Solution
Verified by Experts
Method 1 (Ground frame method)
At the maximum height, both `m_(1)` and `m_(2)` have same velocity as the relative sliding between them stops. Since no external force acts horizontally, linear momentum is conserved in horizontal direction
`(vecp_(x))_(f)=(vecp_(x))_(i)`
where `vecp_(x_(i))=m_(1)v_(0)hati` and `vecp_(x_(f))=(m_(1)+m_(2))vhati`
Then we have `(m_(1)+m_(2))v=m_(1)v_(0)`
WE theorem `W_(ext)+W_("int")=/_\K`
where `W_("ext")=-m_(1)gh, W_("int")=W_("contact")=0, `
and `/_\ K=[1/2(m_(1)+m_(2))v^(2)-(m_(1)v_0^(2))/2]`
This gives `-m_(1)gh=1/2(m_(1)+m_(2))v^(2)-(m_(1)v_(0)^(2))/2`........ii
Sustituting `v` from eqn i and eqn ii we have
`h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
Method 2: (Work energy theorem from centre of mass frame)
The block attains a maximum height when the final relative velociyt `v_(rel)` between block and wedge becomes zero.
that mean `(v_(ref))=0`.
The initial relative velocity betwen block and wedge is given as
`(v_(ref))_(i)=v_(0)`
Substituting `(v_(ref)_(f)=0` and `(v_(rel))_(i)=v_(0)` in the formula.
`/_\K'=1/2mu[(v_(rel)_(f)^(2)-(v_(rel))_(i)^(2)]`
we have `/_\K'=-1/2muv_(0)^(2)`
while ascending through a height `h` (say) the external force, that is the earth's gravity does work on the block `m_(1)` which can be given as:
`W_(ext)(=W_("gravity"))=-m_(1)gh`
The internal (constraint) forces (normal reactions) between `m_(1)` and `m_(2)` as a whole do not performe work, `W_(int)=0`
Finally, putting `/_\K'=-1/2muv_(0)^(2), W_(ext)=-m_(1)gh` and `W_("int")=0` in
We theorem `W_(ext)+W_("int")=/_\K'`
we have `-m_(1)gh+0=-1/2muv_(0)^(2)`
`where mu=(m_(1)m_(1))/(m_(1)+m_(2))`
This gives `h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
At the maximum height, both `m_(1)` and `m_(2)` have same velocity as the relative sliding between them stops. Since no external force acts horizontally, linear momentum is conserved in horizontal direction
`(vecp_(x))_(f)=(vecp_(x))_(i)`
where `vecp_(x_(i))=m_(1)v_(0)hati` and `vecp_(x_(f))=(m_(1)+m_(2))vhati`
Then we have `(m_(1)+m_(2))v=m_(1)v_(0)`
WE theorem `W_(ext)+W_("int")=/_\K`
where `W_("ext")=-m_(1)gh, W_("int")=W_("contact")=0, `
and `/_\ K=[1/2(m_(1)+m_(2))v^(2)-(m_(1)v_0^(2))/2]`
This gives `-m_(1)gh=1/2(m_(1)+m_(2))v^(2)-(m_(1)v_(0)^(2))/2`........ii
Sustituting `v` from eqn i and eqn ii we have
`h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
Method 2: (Work energy theorem from centre of mass frame)
The block attains a maximum height when the final relative velociyt `v_(rel)` between block and wedge becomes zero.
that mean `(v_(ref))=0`.
The initial relative velocity betwen block and wedge is given as
`(v_(ref))_(i)=v_(0)`
Substituting `(v_(ref)_(f)=0` and `(v_(rel))_(i)=v_(0)` in the formula.
`/_\K'=1/2mu[(v_(rel)_(f)^(2)-(v_(rel))_(i)^(2)]`
we have `/_\K'=-1/2muv_(0)^(2)`
while ascending through a height `h` (say) the external force, that is the earth's gravity does work on the block `m_(1)` which can be given as:
`W_(ext)(=W_("gravity"))=-m_(1)gh`
The internal (constraint) forces (normal reactions) between `m_(1)` and `m_(2)` as a whole do not performe work, `W_(int)=0`
Finally, putting `/_\K'=-1/2muv_(0)^(2), W_(ext)=-m_(1)gh` and `W_("int")=0` in
We theorem `W_(ext)+W_("int")=/_\K'`
we have `-m_(1)gh+0=-1/2muv_(0)^(2)`
`where mu=(m_(1)m_(1))/(m_(1)+m_(2))`
This gives `h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. Q. The time taken by the block to reach the ground is:
A wedge of mass 4m is initially at rest on frictionles horizotnal surface. A small block of mass m moving with speed v_(0) and climbs on wedge. Find maximum height achieved by block
A long block A of mass M is at rest on a smooth horizontal surface.A small block B of mass M//2 is placed on A at one end and projected along A with some veklocity v.The coefficient of friction between the block is mu then , the accelerations of blocks A and B before reaching a common velocity will be respectively
Figure shows a block A of mass 6 m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
A body of mass M with a small block m placed on it rests on a smooth horizontal surface. The block is set in motion in the horizontal direction with a velocity v . To what height relative to the initial level will the block rise after breaking off from the body M . Friction can be assumed to be absent.
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. The horizontal force applied on the wedge is:
A wedge of mass m1 with its upper surface hemispherical in shape, as shown in Fig. 4E. 7 (a), rests on a smooth horizontal. surface near thewall. A small block of mass m2 slides without friction on the hemispherical surface of the wedge. What is the 'maxi.mum velocity attained by the wedge ?
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. Q. The normal reaction between wedge and block is:
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. Q. The normal reaction offered by ground to the wedge is: