Home
Class 11
PHYSICS
Two point prticles A and B are placed in...

Two point prticles `A` and `B` are placed in line on frictionless horizontal plane. If particle `A` (mass `1 kg`) is move with velocity `10 m//s` towards stationary particle `B` (mass `2kg`) and after collision the two move at an angle of `45^(@)` with the initial direction of motion, then find

a. velocites of `A` and `B` just after collision.
b. coefficient of restitution

Text Solution

Verified by Experts

The very first step to solve such problems is to find the line of impact which is along the direction of force applied by `A` on `B`, resulting the stationary particle `B` to move. Thus, by watching the direction of motion of `B`, line of impact can be determined. in this case, the line of impact is along the direction of motion of `B` i.e. `45^(@)` with the initial diretion of motion of `A`.
a. Let us apply the principle of conservation of momentum.
Along `x-`direction:
`m_(A)u_(A)=m_(A)v_(A)cos45^(@)m_(B)v_(B)cos45^(@)`
or `1(10)=1(v_(A)cos45^(@))+2(v_(B)cos45^(@))`
or `v_(A)+2v_(B)=10sqrt(2))` ..........i
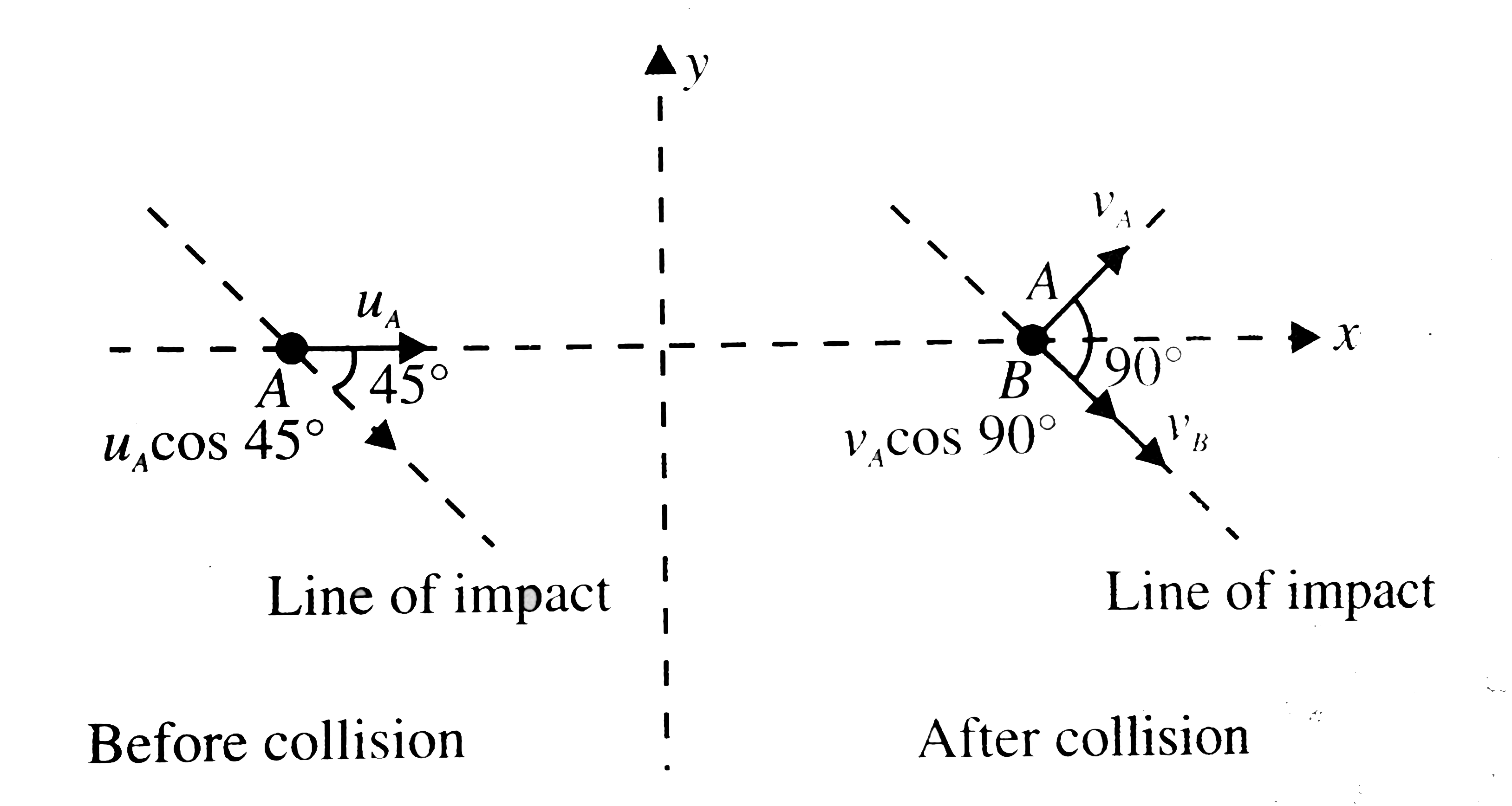
Along `y` direction
`0=m_(A)v_(A)sin45^(@)-m_(B)v_(B)sin45^(@)`
or `0=1(v_(A)sin45^(@))-2(v_(B)sin45^(@))`
or `v_(A)=2v_(B)`
Solving the two equation `v_(A)=10/(sqrt(2))m//s` and `v_(B)=5/(sqrt(2))m//s`
b. coefficient of restitution
`e=("velocity of separation along line of impact")/("velocity of approach along line of impact")`
`=(v_(B)-v_(A)cos90^(@))/(u_(A)cos45^(@))=(5/sqrt(2)-0)/(10/sqrt(2))=1/2`
hence, `P` is constant.
Promotional Banner

Topper's Solved these Questions

  • CENTRE OF MASS

    CENGAGE PHYSICS|Exercise Solved Examples|13 Videos

  • CENTRE OF MASS

    CENGAGE PHYSICS|Exercise Exercise 1.1|20 Videos

  • CALORIMETRY

    CENGAGE PHYSICS|Exercise Solved Example|13 Videos

  • DIMENSIONS & MEASUREMENT

    CENGAGE PHYSICS|Exercise Integer|2 Videos

Similar Questions

Explore conceptually related problems

A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?

A ball moving with a speed of 10" m s"^(-1) strikes an identical ball such that after the collision the direction of each ball makes an angle 45^(@) with the original line of motion. Find the speeds of the two balls after the collision.

A wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e .

A particle of mass m collides with a stationary particle and continues to move at an angle of 45^(@) with respect to the original direction. The second particle also recoils at an angle of 45^(@) to this direction. The mass of the second particle is (collision is elastic)

A particle 1 moving with velocity v= 10m//s experienced a head on collision with a stationary particle 2 of the same mass. As a result of collision, the kinetic energy of the system decreased by 50%. Find the magnitude and direction of the velocity of the particle 1 after collision.

A particle of mass m moving on a smooth surface with velocity 10 m//s strikes another particle of mass 2 m moving with 5 m//s in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.

A particle of mass 2kg moving with a velocity 5hatim//s collides head-on with another particle of mass 3kg moving with a velocity -2hatim//s . After the collision the first particle has speed of 1.6m//s in negative x-direction, Find (a) velocity of the centre of mass after the collision, (b) velocity of the second particle after the collision. (c) coefficient of restitution.

There are two blocks A and B placed on a smooth surface. Block A has mass 10 kg and its is moving with velocity 0.8 m/s towards stationary B of unknown mass. At the time of collision, their velocities are given by the following graph : Coefficient of restitution of the collision is

A ball of mass 1 kg moving with a velocity of "0.4 ms"^(-1) collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms^(1) in a direction making an angle of 90^(@) with its initial direction. The momentum of the second ball after the collision will be (in kg ms^(-1) )