Method 1 (using coservation of linear momentum)
If take wedge and particle as a system, no external impulse acts in horizontal direction, the linear momentum should be constant consrved in horizontal direction. As the particle is moving normal direction, it has no component of velocity in sloping surface direction (tangent direction).
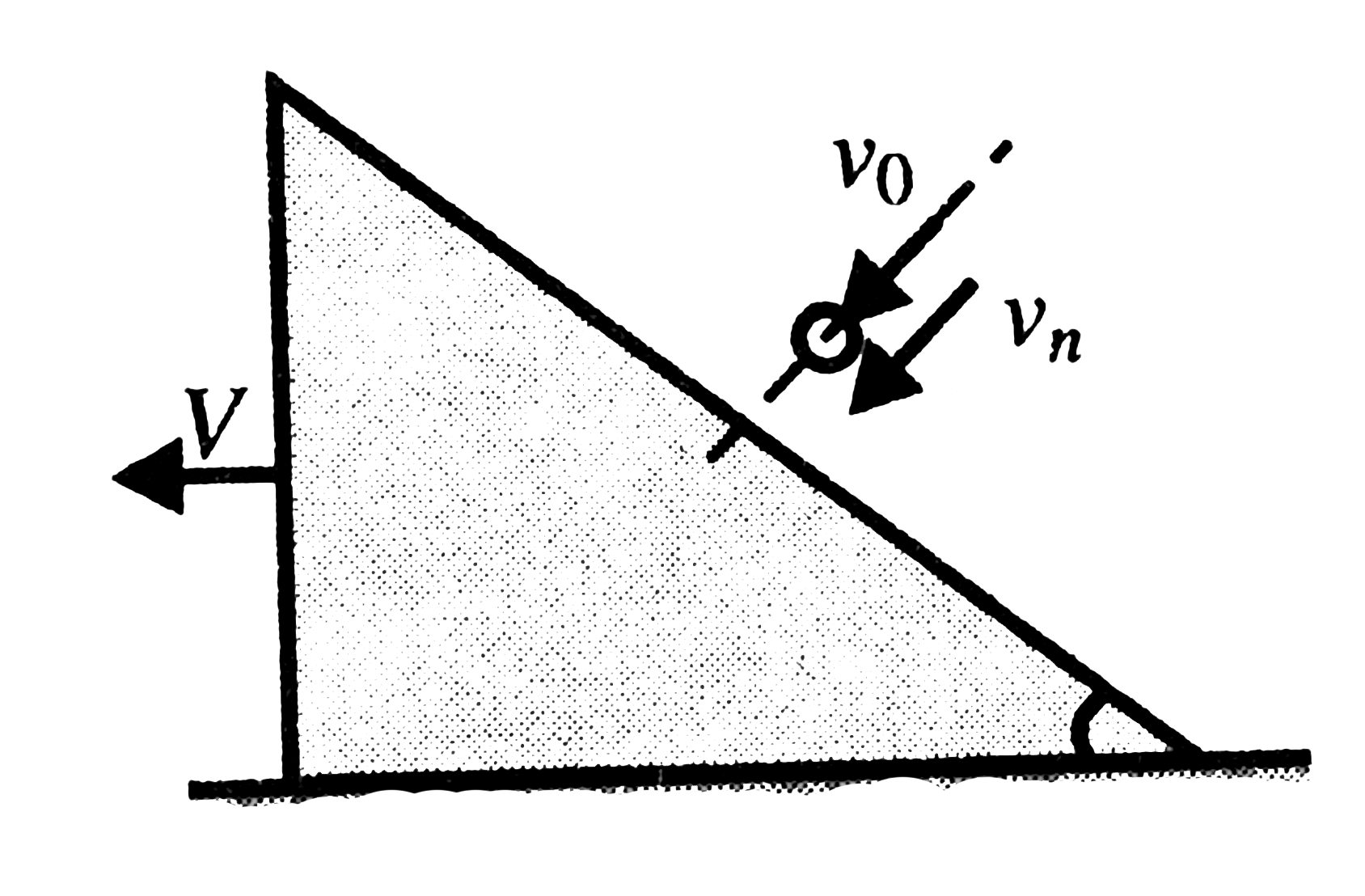
Hence after collision particle will have no velocity component in common tangent direction. the velocity of the particle will confine along common normal direction only. Let velocity of the particle and wedge after collision `v_(n)` and `V` respectively.
Conserving linear momentum in horizontal direction
`mv_(0)sintheta=MV+mv_(n)sintheta`............i
Now, using Newton's law of collision
`(v_(2)-v_(1))_(n)=e(u_(1)-u_(2))`
`(Vsintheta-v_(n))=e(v_(0)-0) ` ..........ii
Solving i and ii we get
`V=((1+e)mv_(0)sintheta)/(M+msin^(2)theta)`
Method 2 (Using impulse method)
The impulse acting on the ball and wedge can be represented as

`Jsintheta=MV`......i
`mv_(J)=mv_(n)`..........ii
And newton's law of restitution
`(vsintheta-v_(n))=e(v_(0)-0)`.........iii
Solving eqn i, ii and iii we get
`V=((1+e)mv_(0)sintheta)/(M+msin^(2)theta)`