Text Solution
Verified by Experts
Topper's Solved these Questions
CENTRE OF MASS
CENGAGE PHYSICS|Exercise Exercise 1.1|20 VideosCENTRE OF MASS
CENGAGE PHYSICS|Exercise Exercise 1.2|23 VideosCENTRE OF MASS
CENGAGE PHYSICS|Exercise INTEGER_TYPE|1 VideosCALORIMETRY
CENGAGE PHYSICS|Exercise Solved Example|13 VideosDIMENSIONS & MEASUREMENT
CENGAGE PHYSICS|Exercise Integer|2 Videos
CENGAGE PHYSICS-CENTRE OF MASS-Solved Examples
- A body of mass 1 kg initially at rest, explodes and breaks into three ...
Text Solution
|
- A wedge of mass m2 is kept on a spring balance. A small block of mass ...
Text Solution
|
- A spring is connected with plank and other end of spring is connected ...
Text Solution
|
- A wedge having a vertical slot in it is placed on smooth horizontal su...
Text Solution
|
- A rope thrown over a pulley has a on one of its ends and a counterbala...
Text Solution
|
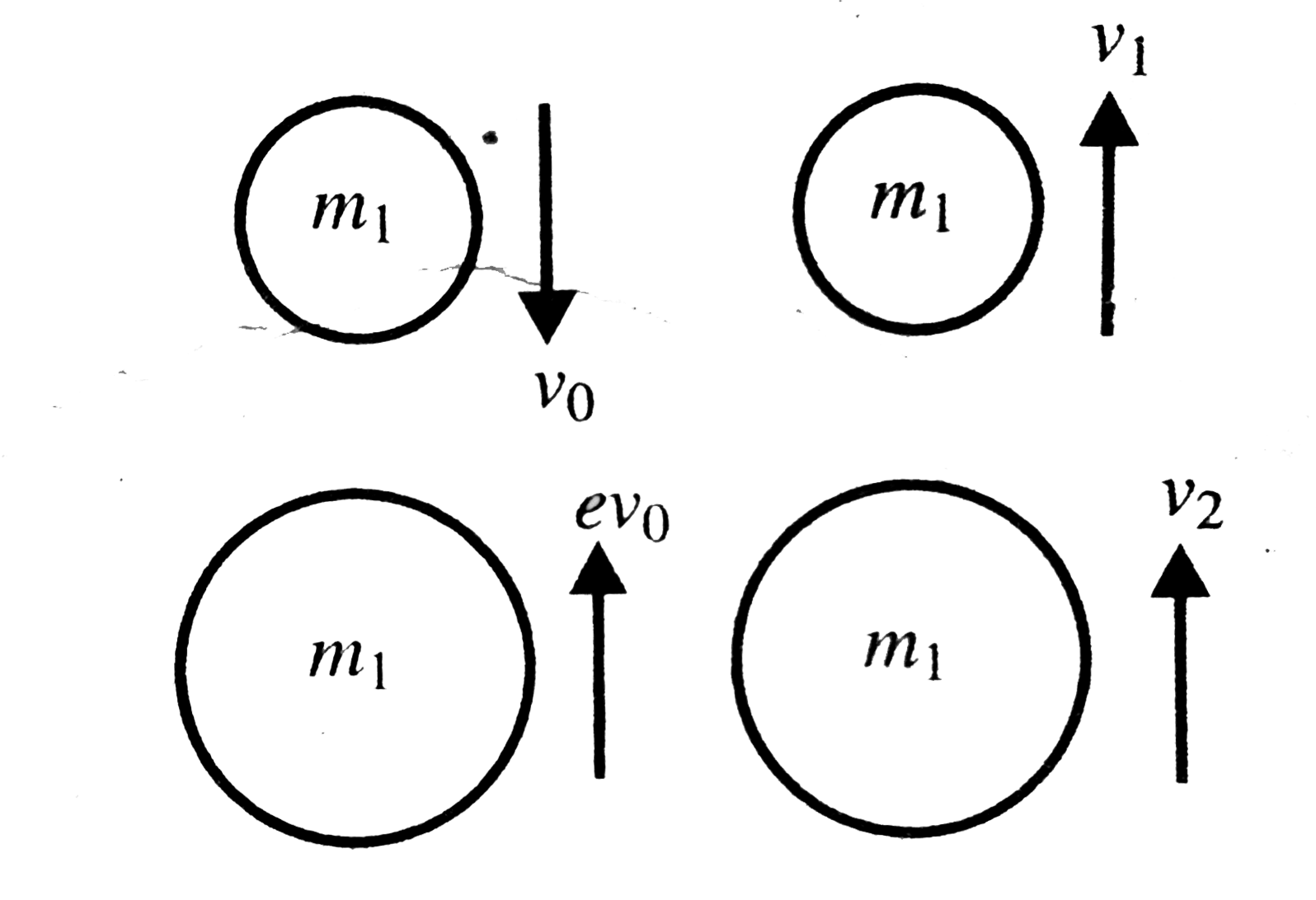
- A block of mass m is relesed from rest from a height h onto a smooth s...
Text Solution
|
- A particle of mass m(1) is projected to the right with speed v(1) onto...
Text Solution
|
- A small ball of mass m is projected with a minimum horizontal velocity...
Text Solution
|
- A bead of mass m kept at the top of a smooth hemispherical wedge of ma...
Text Solution
|
- There are two pendulums with bobs having indencital size and mass. The...
Text Solution
|
- An empty luggage carrier A of mass M=40 kg slide without friction on h...
Text Solution
|
- A ball of mass m is pushed with a horizontal velocity v(0) from one en...
Text Solution
|
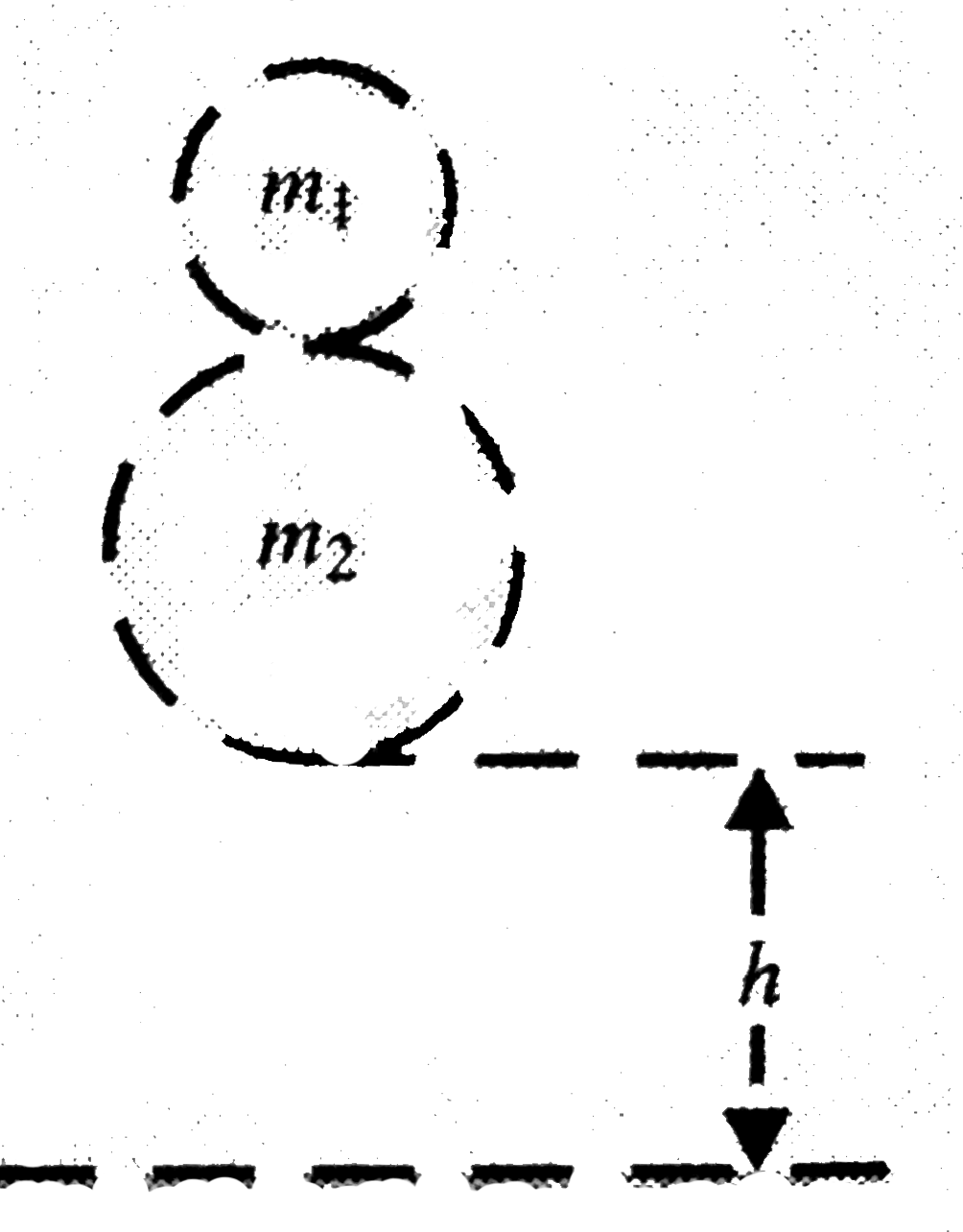
- Two spherical bodies of mass m(1) and m(2) fall freely through a dista...
Text Solution
|