A container `A` is having some fluid of density `theta_(0)`. If is connected with a `U` tbe manometer shown in figure. Find the pressure of the container in both the cases given in figure.

Explanation

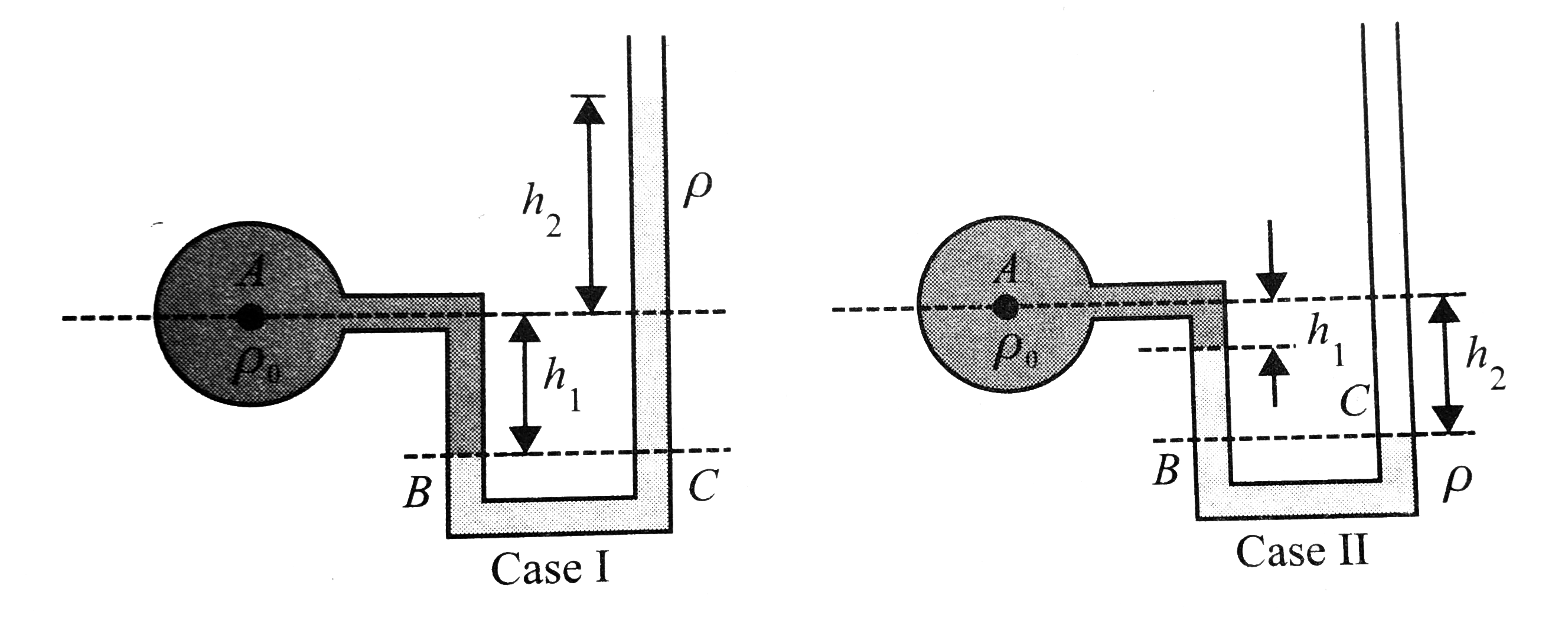
Case I Let the gauge pressure at `A` be `p_(A)`. Starting from container move along the manometer by a height `h_(1)` downwards. The change in pressure will be `=rho_(0)gh_(1)`. The pressur at `B` and `C` will be the same. To move to the open end, we have to move by a distance `(h_(1)+h_(2))` upward. Hence, change in pressure will be `-rhog(h_(1)+h_(2))`. finally , we reach the top, i.e. open to atmosphere. Hence, the manometric equation of the guage pressure will be
`p_(A)+rho_(o)gh_(1)-rhog(h_(1)+h_(2))=0`
`impliesp_(A)=rhog(h_(1)+h_(2))-rho_(0)gh_(1)+p_(0)`
Case II Gauge pressure at `A`, `p_(A)+rho_(0)gh_(1)+rhog(h_(2)-h_(1))=0`
Absolute pressure at `A` `p'A=rho_(0)gh_(1)+rhog(h_(2)-h_(1))=p_(0)`