Water and liquid are filled up behind a square wall of side. Find out
a. pressures at `A, B` and `C`
b. forces in part `AB` and `BC`
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
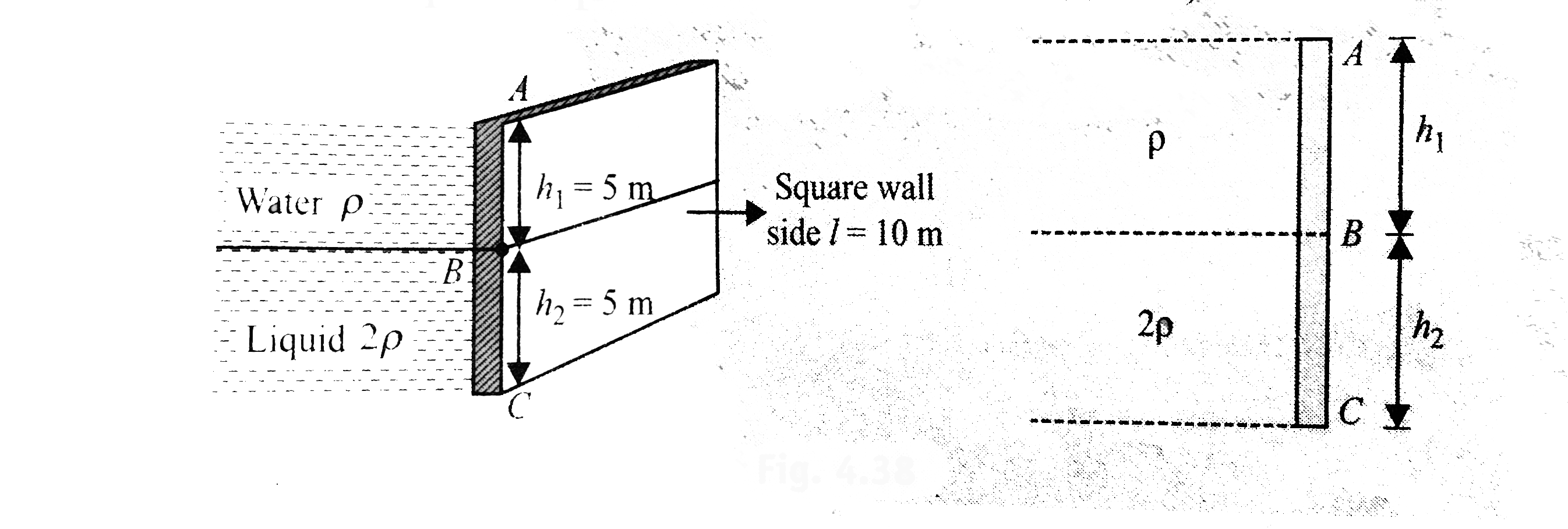
Water and liquid are filled up behind a square wall of side. Find out
a. pressures at `A, B` and `C`
b. forces in part `AB` and `BC`
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
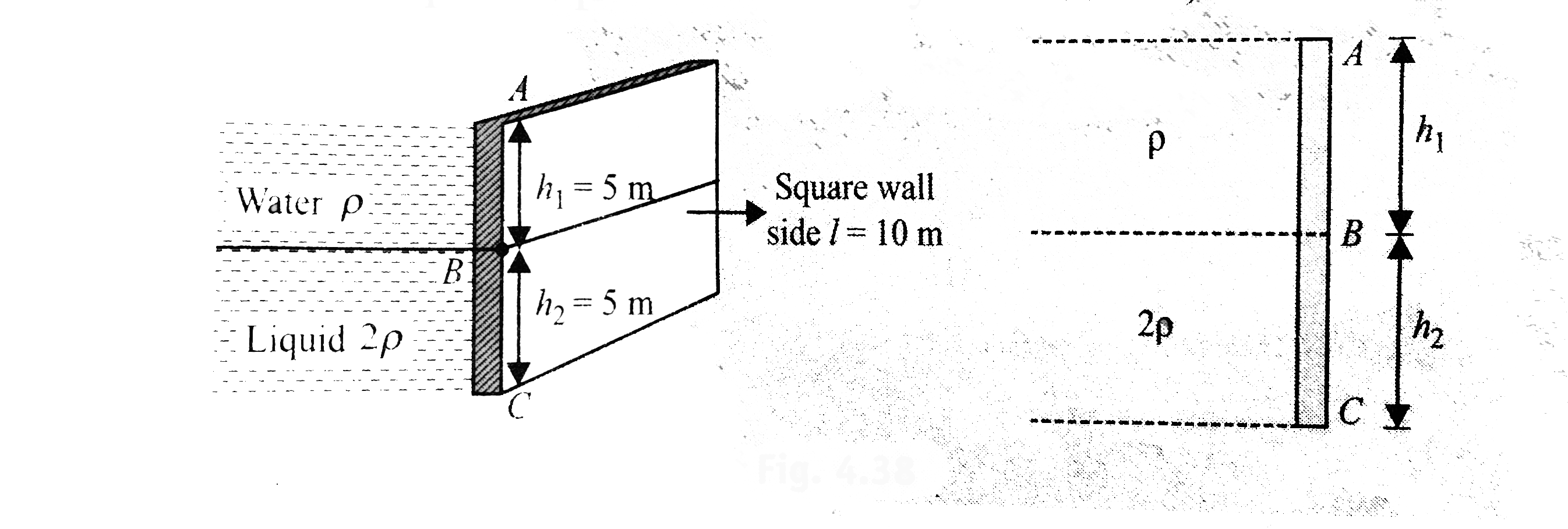
a. pressures at `A, B` and `C`
b. forces in part `AB` and `BC`
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
Text Solution
Verified by Experts
As there is no liquid above `A`
pressure at `A` is `p_(A)=0`
Pressure at `B` is `p_(B)=rhogh_(1)`
pressure at `C` is `p_(C)=rhogh_(1)+2rhogh_(2)`
b. Force at `A` is zero. Take a strip a of width `dx` at a depth `'x'` in part `AB`. Pressure is equal to `rhogx`.
Force on strip `=` pressure `xx` area

`dF=rhogldx`
Total force up to `B`,
`F_(B)=int_(0)^(h)rhog ldx=(rhoglh_(1)^(2))/2`
`=(1000xx10xx10xx5xx5)/2=1.25xx10^(6)N`
In part `BC` for force take a elementary strip of width `dx` in portion `BC`. Pressure is givenby
`rhogh_(1)+2rhog(x-h_(1))`
Force on the elementary strip `=` pressure `xx` area
`:.dF=[rhogh_(1)+2rhog(x-h_(1))]ldx`
The limit of `x` will be `x=h_(1)` to `x=h_(1)+h_(2)=l`

The force on part `BC` is `F=int_(h_(1))^(h_(1)+h_(2))[rhogh_(1)=2rhog(x-h-10]l`
But `h_(1)+h-2=l=[rhogh_(1)x+2rhog[(x^(2))/2-h_(1)x]]_(h_(1))^l`
`=rhogh_(1)h_(2)l+rhogl(l-h_(1))^2`
`=rhogh_(2)l[h_(1)+h_(2)]=rhogh_(2)l^(2)`
`=1000xx10xx5xx10xx10`
`=5xx10^(6)N`
c. Method 1
Total `=5xx10^(6)+1.25xx10^(6)=6.25xx10^(6)N`
Taking torque about `A` the total torque of force in `AB` is
`intdx=int_(0)^(F)rhogxldxx`
`[(rhoglx^(3))/3]_(0)^(h_(1))=(rhoglh_(1)^(3))/3=(1000xx10xx10xx125)/3`
`=(1.25xx10^(7))/3Nm`
The total torque of force in `BC` about `A` is given by
`intdFx=int_(R)^(l)[rhogh_(1)+2rhog(x-h_(1))]ldx.x`
`rhogh_(1)h_(2)l[h_(1)+(h_(2))/2]+rhogh_(2)^(2)l[h_(1)+(2h_(2))/3]`
`=2.5xx7.5xx10^(6)+62.5/3xx10^(6)`
`118.75/3xx10^(6)Nm`
Total torque `=(11.875xx10^(7))/3+(1.25xx10^(7))/3`
`=(13.125xx10^(7))/3Nm`
Total torque `=` Total force `xx` Distance of point of application of force from top `= Fx_(p)`
`implies 6.25xx10^(6)x_(p)=(13.125xx10^(7))/3Nm`
`implies x_(p)=7m`
Method 2. Pressure diagram on the wall
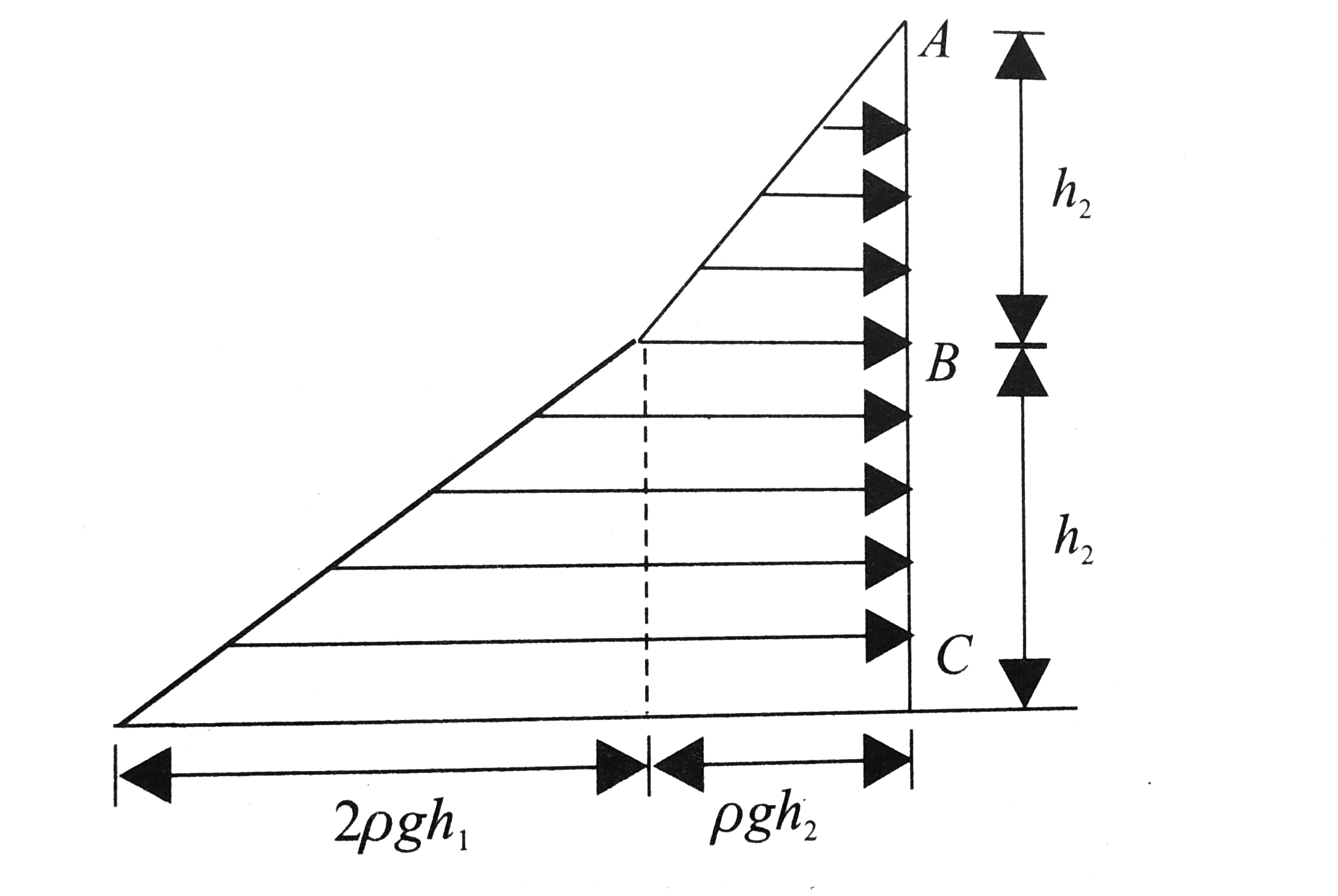
Total force on the wall per unit width of the wall `=` Area of presure diagram.
`F/b=1/2(rhogh_(1))h_(1)+rhogh_(1)h_(2)+1/2(2rhogh_(2))h_(2)`
`=rhog[(h_(1)^(2))/2+h_(2)^(2)]+rhogh_(1)h_(2)`
`F_(del)=F=1/2rhog_(1)^(2)+rhoglh_(2)[h_(1)+h_(2)]`
`6.25xx10^(6)N`
Total force on `AB` part `F_(AB)=1/2rhoglh_(1)=1.25xx10^(6)N`
Total force on `BC` part `F_(BC)=rhoglh_(2)(h_(1)+h_(2))=5xx10^(6)N` The total force will act at the centroid of the pressure diagram. Let the distance of centroid of pressure diagram be `'r'` from `A`
`r=(rhogh_(1)^(2))/2xx2/3h_(1)+(2rhogh_(2)^(2))/2(h_(1)+2/3h_(2)) +(rhogh_(1)h_(2))(h_(1)+h_(2)/2))/((rhogh_(1)^(20)/2+rhoh_(2)^(2)+rhogh_(1)h_(2))`
`=((h_(1)^(3))/3+h_(2)^(2)(h_(1)+2/3h_(2))+h_(1)h_(2)(h_(1)+(h_(2))/2))/((h_(1)^(2))/2+h_(2)^(2)+h_(1)^(2))`
`r=([1/3+(1+2/3)+(1+1/2)]5)/(1/2+1+1)=(7/2)/(5/2)xx5=7m`
pressure at `A` is `p_(A)=0`
Pressure at `B` is `p_(B)=rhogh_(1)`
pressure at `C` is `p_(C)=rhogh_(1)+2rhogh_(2)`
b. Force at `A` is zero. Take a strip a of width `dx` at a depth `'x'` in part `AB`. Pressure is equal to `rhogx`.
Force on strip `=` pressure `xx` area

`dF=rhogldx`
Total force up to `B`,
`F_(B)=int_(0)^(h)rhog ldx=(rhoglh_(1)^(2))/2`
`=(1000xx10xx10xx5xx5)/2=1.25xx10^(6)N`
In part `BC` for force take a elementary strip of width `dx` in portion `BC`. Pressure is givenby
`rhogh_(1)+2rhog(x-h_(1))`
Force on the elementary strip `=` pressure `xx` area
`:.dF=[rhogh_(1)+2rhog(x-h_(1))]ldx`
The limit of `x` will be `x=h_(1)` to `x=h_(1)+h_(2)=l`

The force on part `BC` is `F=int_(h_(1))^(h_(1)+h_(2))[rhogh_(1)=2rhog(x-h-10]l`
But `h_(1)+h-2=l=[rhogh_(1)x+2rhog[(x^(2))/2-h_(1)x]]_(h_(1))^l`
`=rhogh_(1)h_(2)l+rhogl(l-h_(1))^2`
`=rhogh_(2)l[h_(1)+h_(2)]=rhogh_(2)l^(2)`
`=1000xx10xx5xx10xx10`
`=5xx10^(6)N`
c. Method 1
Total `=5xx10^(6)+1.25xx10^(6)=6.25xx10^(6)N`
Taking torque about `A` the total torque of force in `AB` is
`intdx=int_(0)^(F)rhogxldxx`
`[(rhoglx^(3))/3]_(0)^(h_(1))=(rhoglh_(1)^(3))/3=(1000xx10xx10xx125)/3`
`=(1.25xx10^(7))/3Nm`
The total torque of force in `BC` about `A` is given by
`intdFx=int_(R)^(l)[rhogh_(1)+2rhog(x-h_(1))]ldx.x`
`rhogh_(1)h_(2)l[h_(1)+(h_(2))/2]+rhogh_(2)^(2)l[h_(1)+(2h_(2))/3]`
`=2.5xx7.5xx10^(6)+62.5/3xx10^(6)`
`118.75/3xx10^(6)Nm`
Total torque `=(11.875xx10^(7))/3+(1.25xx10^(7))/3`
`=(13.125xx10^(7))/3Nm`
Total torque `=` Total force `xx` Distance of point of application of force from top `= Fx_(p)`
`implies 6.25xx10^(6)x_(p)=(13.125xx10^(7))/3Nm`
`implies x_(p)=7m`
Method 2. Pressure diagram on the wall

Total force on the wall per unit width of the wall `=` Area of presure diagram.
`F/b=1/2(rhogh_(1))h_(1)+rhogh_(1)h_(2)+1/2(2rhogh_(2))h_(2)`
`=rhog[(h_(1)^(2))/2+h_(2)^(2)]+rhogh_(1)h_(2)`
`F_(del)=F=1/2rhog_(1)^(2)+rhoglh_(2)[h_(1)+h_(2)]`
`6.25xx10^(6)N`
Total force on `AB` part `F_(AB)=1/2rhoglh_(1)=1.25xx10^(6)N`
Total force on `BC` part `F_(BC)=rhoglh_(2)(h_(1)+h_(2))=5xx10^(6)N` The total force will act at the centroid of the pressure diagram. Let the distance of centroid of pressure diagram be `'r'` from `A`
`r=(rhogh_(1)^(2))/2xx2/3h_(1)+(2rhogh_(2)^(2))/2(h_(1)+2/3h_(2)) +(rhogh_(1)h_(2))(h_(1)+h_(2)/2))/((rhogh_(1)^(20)/2+rhoh_(2)^(2)+rhogh_(1)h_(2))`
`=((h_(1)^(3))/3+h_(2)^(2)(h_(1)+2/3h_(2))+h_(1)h_(2)(h_(1)+(h_(2))/2))/((h_(1)^(2))/2+h_(2)^(2)+h_(1)^(2))`
`r=([1/3+(1+2/3)+(1+1/2)]5)/(1/2+1+1)=(7/2)/(5/2)xx5=7m`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Water and liquid is filled up behind a square wall of side l Find out (a). Pressure at A, B and C (b). Forces in part AB and BC (c). Total force and point of application of force. (Neglect atmosphere pressure in every calculation.)
Hydrostatics: Pressure due to a Liquid Column | Equating pressure in U-tube Problems | Force and Torque on container wall (point of application of force)
In a given arrangement (a) find out velocity of water coming out of C (b). Find out pressure A, B and C
Three force are applied to a square plate as shown in the figure. Find the magnitude, direction and point of application of the resultant force if this point is taken on the side BC .
Mercury is completely filled in a rectangular take of height 72 cm. The atmospheric pressure at the place is 72 cm. of Hg. Find the distance in cm of point of application from bottom of tank of the net force , on the inner surface of the side vertical wall of tank.
Three forces are applied to a square plate as shown in Figure. Find the modulus, direction, and the point of application of the resultant force, if this point is taken on the side BC.
Two liquids of densities p_(1) and p_(2) (p2_= 6 p1 ) are filled up behind a square wall of side 8 m as shown in figure. The liquids have height as shown. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)
A capillary tube is dipped in a liquid. Let pressure at point A,B and C be p_(A)p_(B) and p_(C) respectively, then