a. Vertical thrust of the liquid is equal to weight of the liquid column above the curve (spherical) surface i.e.
`F_V=Vrhog`
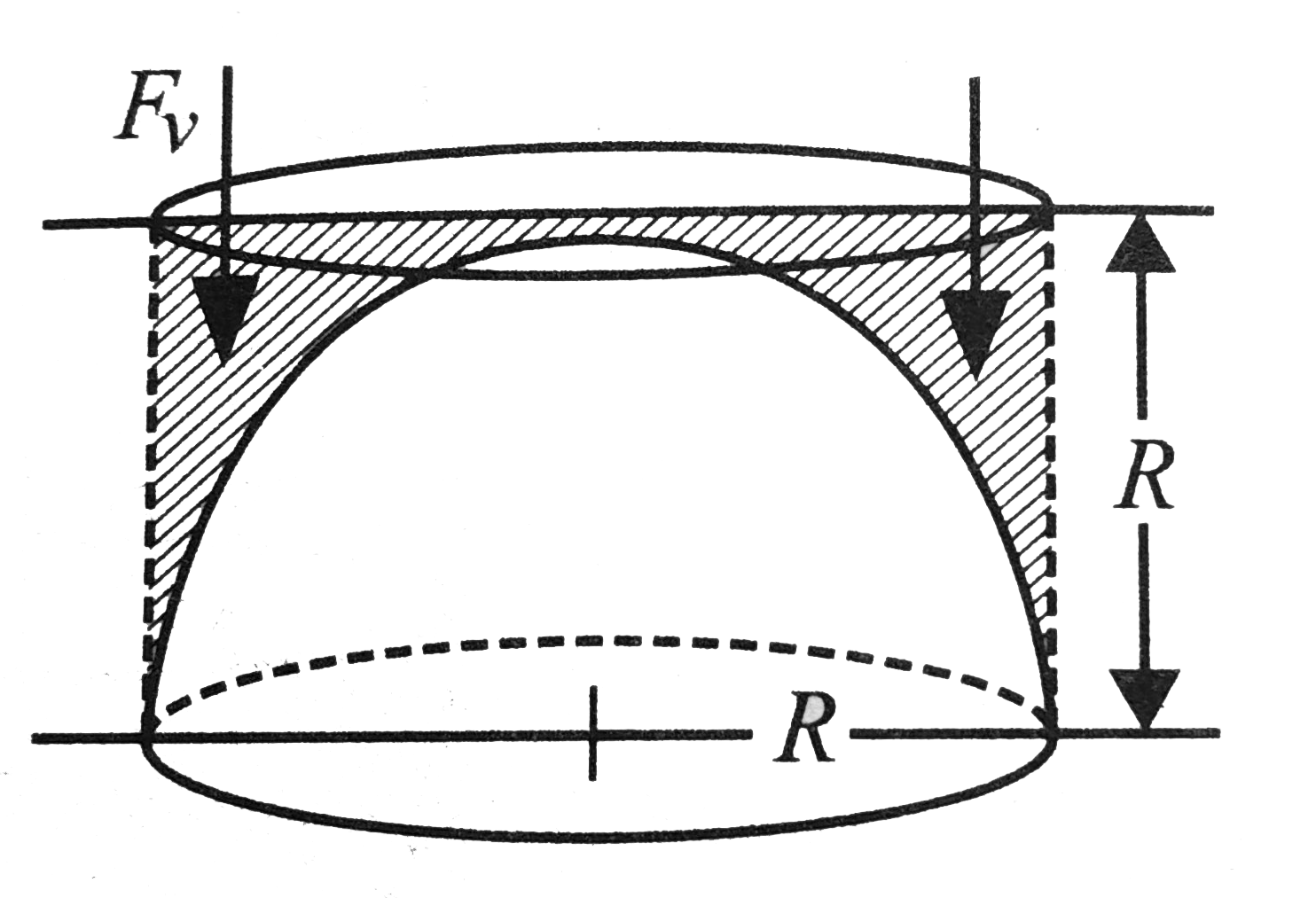
where `V=` volume of the shaded portion
`=` Volume of the cylinder `-` volume of the hemisphere
`=(piR^(2))R=2/3piR^(3)=(piR^(3))/3`
Substituting `V` in the equation `F_(v)=Vrhog`, we have
`F_(v)=(piR^(3))/3rhog` (down)
b. The upward thrust on the base of the hemisphere is
`F_(V)^(')=V^(')rhog`
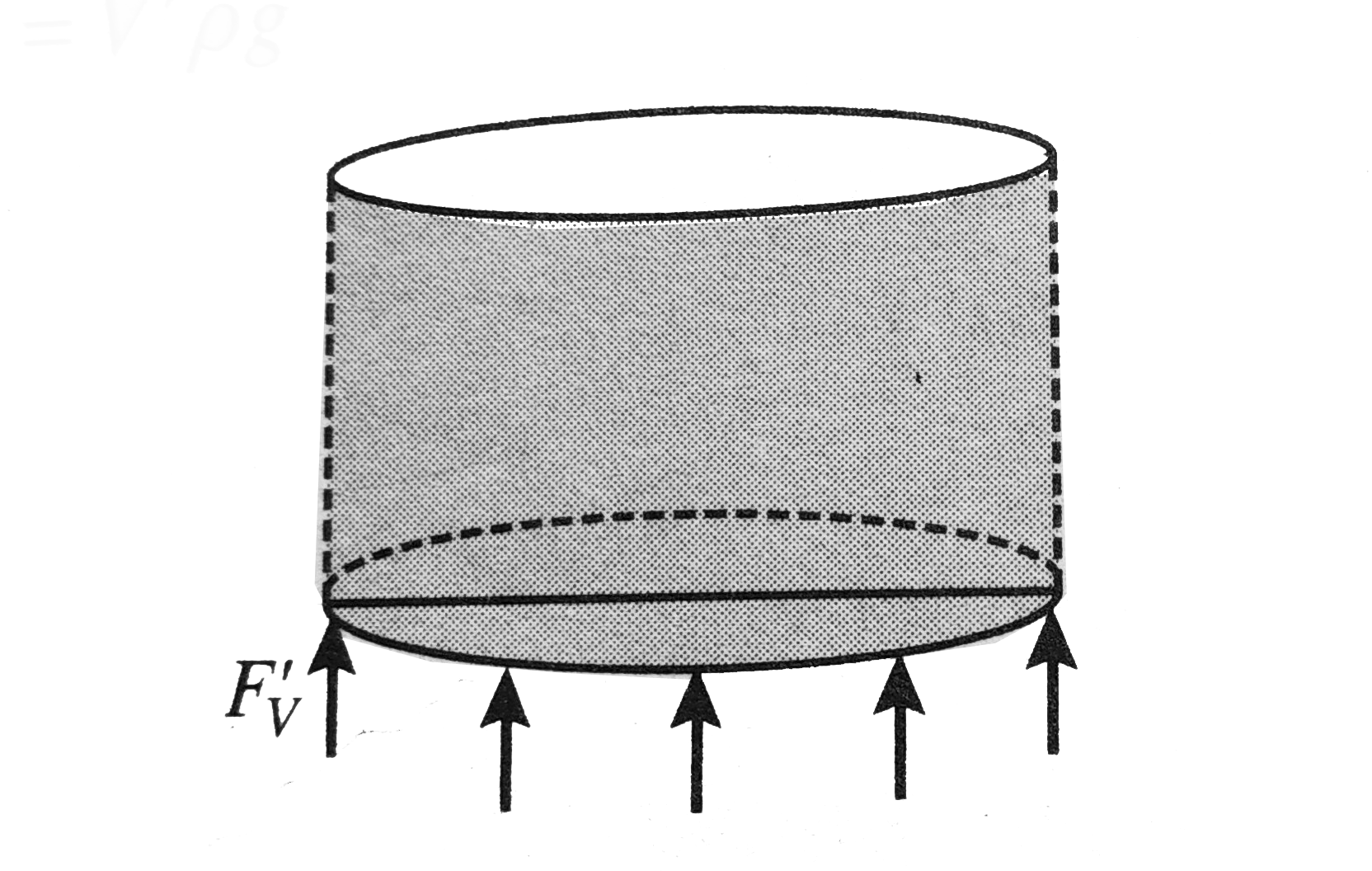
where `V'=` Volume of the liquid column above the base
`=(piR^(2))R=piR^(3)`. Then we have `F_(v)^(')=piR^(3)rhog` ( upward)
c. Side Thrust `F_(h)=0` (as discussed earlier)
d. The total hydrostatic force is
`F=F_(v)^(')-F_(v)`
`=piR^(3)rhog-(piR^(3))/3rhog=1/3piR^(2)rhog` (upward)