A cylindrical vessel of diameter `0.3 m` and height `0.6 m` is filled two thirds with a liquid of specific gravity `0.8`. The vessel is rotated about its axis. a. Determine the speed of rotation when the liquid just starts spilling. b.Find the speed of rotation when the base is just visible. c. What is the percentate of liquid left in the vessel?

Explanation

Initial height of liquid in the vessel `y=0.6xx2/3=0.4m`

Height of the container `=0.6m`
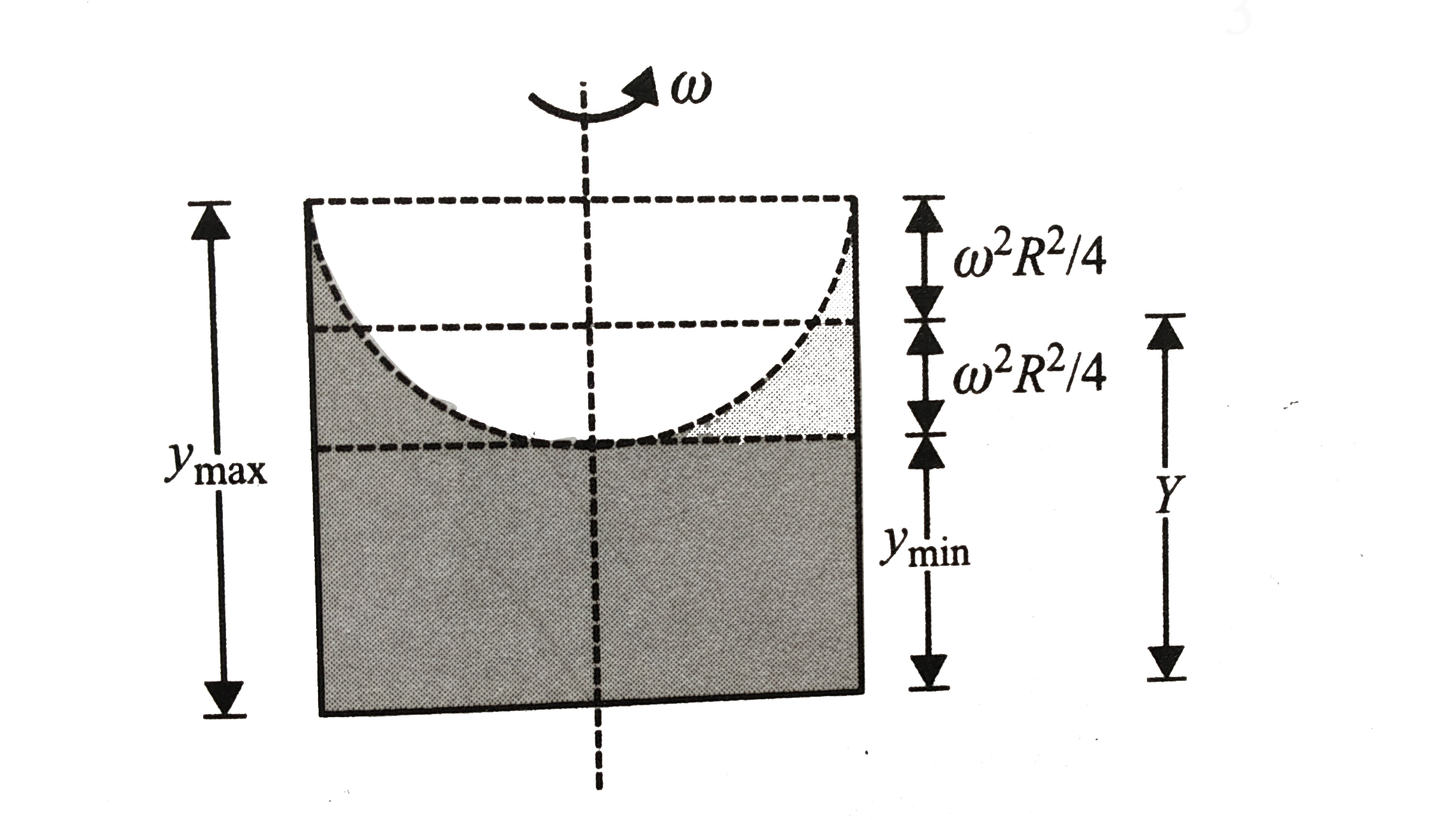
`y_("max")-y_("min")=(omega^(2)R^(2))/(2g)`……….i
`y_("max")=y+(omega^(2)R^(2))/(4g)`…………ii
`y_("min")=y-(omega^(2)R^(2))/(4g)`.........ii
`y_("min")=y=(omega^(2)R^(2))/(4g)`..........iii
a. `y_("max")=0.6m`
From eqn ii `0.6=0.4+(omega^(2)xx(0.3/2)^(2))/(4xx9.81)`
b. `y_("max")=0.6m, y_("min")=0impliesy_("max")=(R^(2)omega^(2))/(2g)`
`=0.6=((0.3)^(2)xxomega^(2))/(8xx9.81)implies omega=22.9rad//s`
c. The volume of paraboloid of revolution is hal the volume of the enclosing cylinder. volume of the liquid left in the vessel `=(1/2)xx0.6xxA`, where `A` is cross sectional area. Initial volume was `0.4Am^(3)`. Percentage of the liquid left `=(0.3A)/(0.4A)xx100=75%`