The side wall of a wide vertical vessel of height `h=75 cm` a narrow slit (vertical) running all the way down to the bottom of the vessel.
The length of the slit is `l=50 cm` and the width is `b=1 mm`. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt 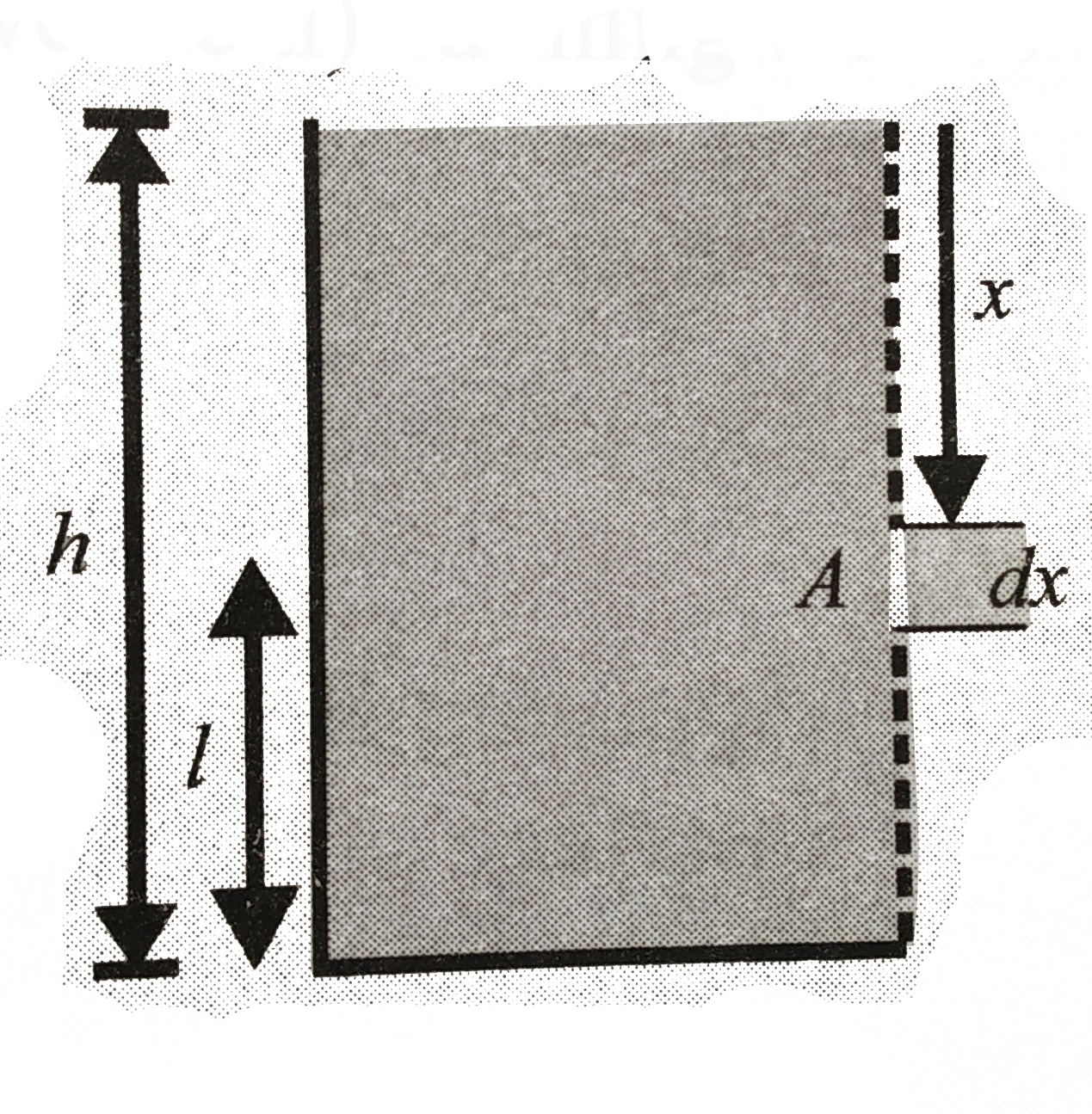
The side wall of a wide vertical vessel of height `h=75 cm` a narrow slit (vertical) running all the way down to the bottom of the vessel.
The length of the slit is `l=50 cm` and the width is `b=1 mm`. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt
The length of the slit is `l=50 cm` and the width is `b=1 mm`. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt

Text Solution
Verified by Experts
Let us consider an infinitensimal portion of length `dx` of the slit at a depth `x` below water level. Reaction force due to this portion is given by
`dF=Av^(2)rho=(bdx)2gxrho`
Total reaction force is
`F=intdf=int_(h-t)^(h)2grhob(xdx)`
`=(2grhob)/2[h^(2)-(l-h)^(2)]=grhobl(2h-l)`
`dF=Av^(2)rho=(bdx)2gxrho`
Total reaction force is
`F=intdf=int_(h-t)^(h)2grhob(xdx)`
`=(2grhob)/2[h^(2)-(l-h)^(2)]=grhobl(2h-l)`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A cylinder of height h = 1 m has a narrow vertical slit along its wall running up to a length l = 40 cm from the bottom. The width of the slit b = 1 mm. The cylinder is filled with water with the slit closed. Find the force experienced by the vessel immediately after then slit is opened?
A thin equiconvex glass lens (mu_(g)=1.5) is beign placed on the top of a vessel of height h=20cm as shown figure. A luminous point source is beign placed at the bottom of vessel on the principal axis of the lens. When the air is on both the side of the lens the image of luminous source is formed at a distance of 20cm from the lens out side the vessel. When the air inside the vessel is being replaced by a liquid of refractive index mu_(l) the image of the same source is being formed at a distance 30cm from the lens outside the vessel. Find the mu_(l) .
Water flows out of a big tank along a tube bent at right angles, the inside radius of the tube is equal to r=0.50cm (figure). The length of the horizontal section of the tube is equal to l=22cm . The water flow rate is Q=0.50 litres per second. Find the moment of reaction forces of flowing water, acting on the tube's walls, relative to the point O.
On the opposite sides of a wide vertical vessel filled with water two identical holes are opened each having the cross-sectional area S=0.50cm^(2) the height difference between them is equal to Deltah=51cm find the resultant force of reaction of the water flowing out of the vessel.
On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to h . Find the resultant force of reaction of water flowing out of vessel.
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice. [Take atmospheric pressure =1.0xx10^5N//m^2 , density of water=1000kg//m^3 and g=10m//s^2 . Neglect any effect of surface tension.]
Figure. Illustrates the interference axperiment with Fresnel mirrors. The angle between the mirrors is alpha = 12' the distance from the mirrors intersection line to the narrow slit S and the screen Sc are equal to r= 10.0 cm and b = 130 cm resoectively. the wavelength of light is lambda = 0.55 mu m . Find: (a) the width of a fringe on the screen and the number of possible maxima, (b) the shift of the interference pattern on the screen when the slit is displaced by del l = 1.0 mm along the are of radius r with centre at the point O , (c) at what maximum width del_(max) of the slit the interference fringes on the screen are still observed sufficiently sharp.
Shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h_(0) and pressure 2p_(0) where p_(0_ is the atmospheric pressure. There is a hole in the wall of tank at a depth h_(1) below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h_(2) of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.
Water leaks out from an open tank through a hole of area 2mm^2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis 0.4 m^2 . The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt. d. From the result of part c. find the time required for half of the water to leak out.