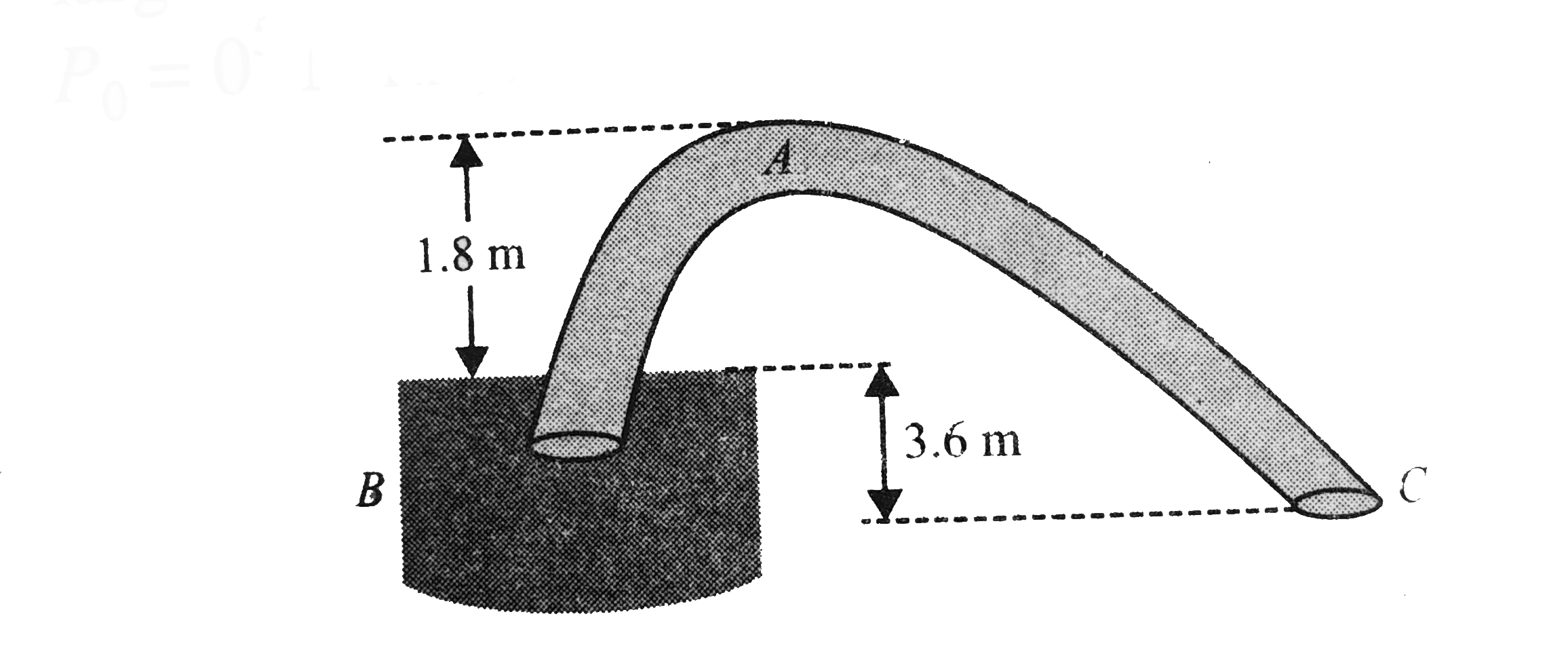
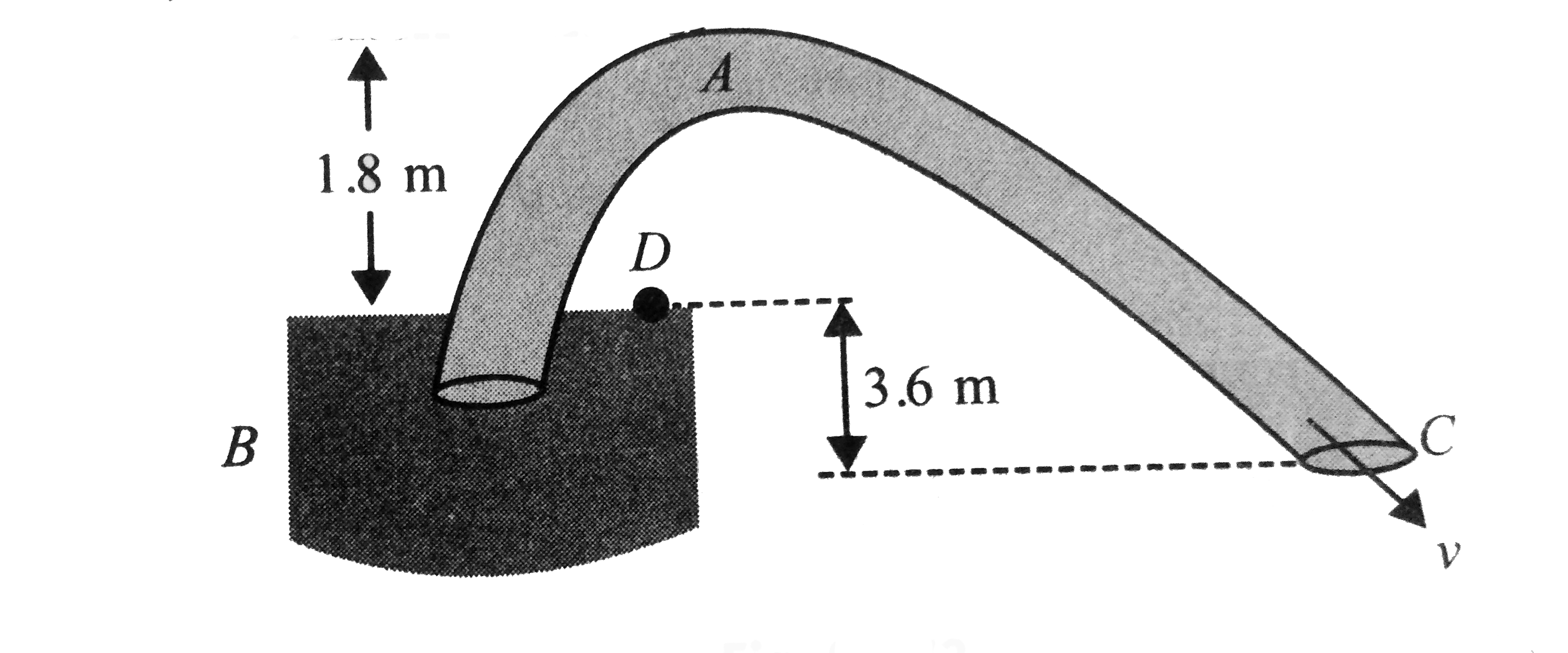
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
FLUID MECHANICS
CENGAGE PHYSICS|Exercise Assertion-Reasoning|8 VideosFLUID MECHANICS
CENGAGE PHYSICS|Exercise Linked Comprehension|43 VideosFLUID MECHANICS
CENGAGE PHYSICS|Exercise Single Correct|95 VideosDIMENSIONS & MEASUREMENT
CENGAGE PHYSICS|Exercise Integer|2 VideosGRAVITATION
CENGAGE PHYSICS|Exercise INTEGER_TYPE|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-FLUID MECHANICS-Multipe Correct
- A liquid flows through a horizontal tube. The velocities of the liquid...
Text Solution
|
- A cylindrical vessel of 90 cm height is kept filled up to the brim. It...
Text Solution
|
- A non-viscous liquid is flowing through a non-uniform pipe from sectio...
Text Solution
|
- A spring balance reads W(1) when a ball is suspended from it. A weighi...
Text Solution
|
- A wooden block is floating in a water tank. The block is pressed to it...
Text Solution
|
- Choose the correct statements from the following:
Text Solution
|
- A body floats in a liquid contained in a beaker. The whole system as s...
Text Solution
|
- Water is flowing smoothly through a closed-pipe system. At one point t...
Text Solution
|
- A siphon has a uniform circular base of diameter 8//sqrt(pi) cm with i...
Text Solution
|
- The difference of pressure between two points along a horizontal pipe ...
Text Solution
|
- A liquid is filled upto height h in a vessel, as shown. Find correct o...
Text Solution
|
- The area of two holes A and B are 2a and a, respectively, The holes ar...
Text Solution
|
- Statement I: When a body floats such that its parts are immersed into ...
Text Solution
|
- Statement I: Imagine holding two identical bricks under water. Brick A...
Text Solution
|
- Statement I: A hydrogen-filled balloon stops rising after it has attai...
Text Solution
|