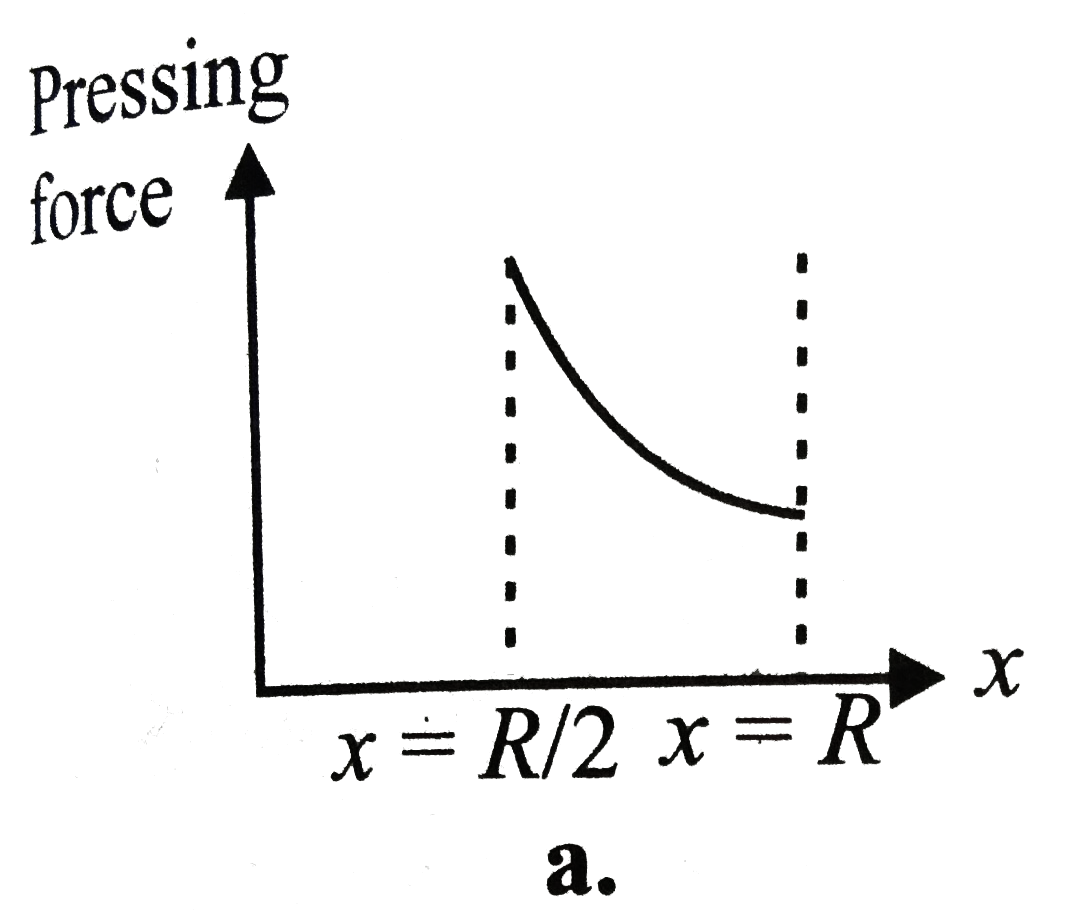
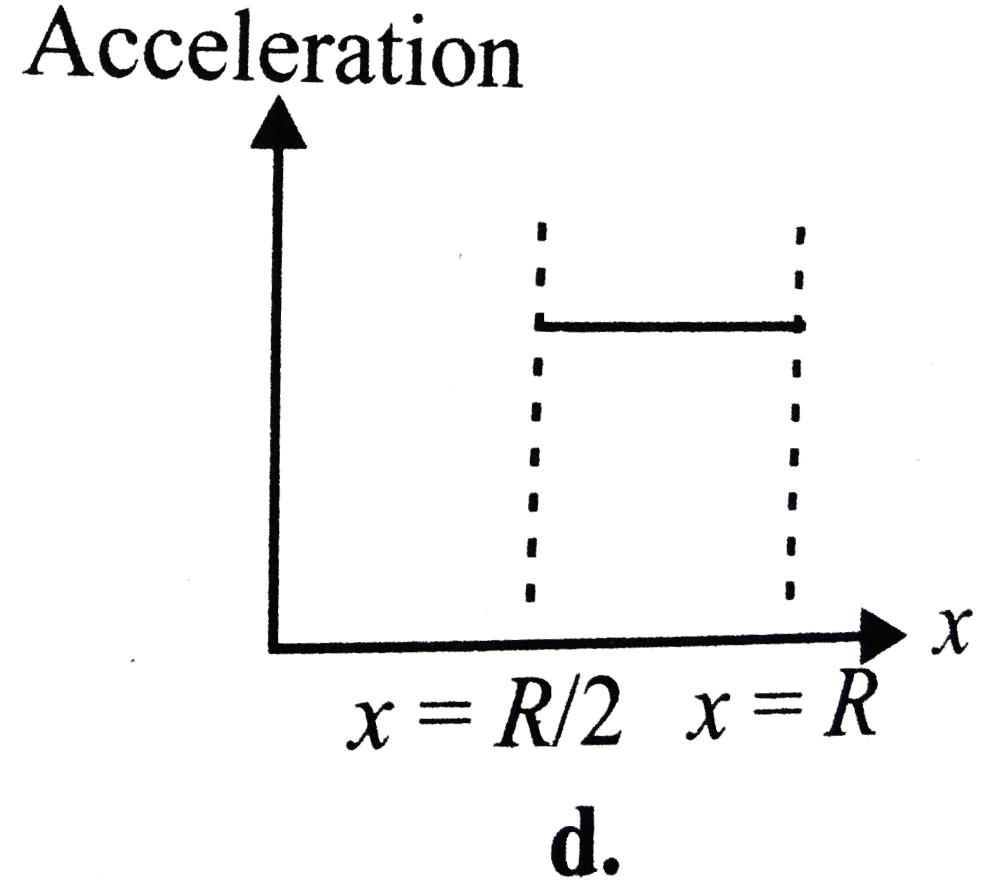
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-GRAVITATION-Single Correct
- Two rings having masses M and 2M respectively, having the same radius ...
Text Solution
|
- A point mass m is released from rest at a distance of 3R from the cent...
Text Solution
|
- A body is thrown from the surface of the earth with velocity (gR(e))//...
Text Solution
|
- The gravitational force exerted by the Sun on the Moon is about twice ...
Text Solution
|
- A tunnel has been dug into a solid sphere of non-uniform mass density ...
Text Solution
|
- A ring having non-uniform distribution of mass M and radius R is being...
Text Solution
|
- An artificial satellite of the earth is launched in circular orbit in ...
Text Solution
|
- A satellite is orbiting around the earth in a circular orbit of radius...
Text Solution
|
- Figure shows the kinetic energy (E(k)) and potential energy (E(p)) cur...
Text Solution
|
- A double star is a system of two stars of masses m and 2m, rotating ab...
Text Solution
|
- A tunnel is dug along a chord of the earth at a perpendicular distance...
Text Solution
|
- Consider a planet moving in an elliptical orbit around the Sun. The wo...
Text Solution
|
- Which of the following statements are true about acceleration due to g...
Text Solution
|
- Let V and E denote the gravitational potential and gravitational field...
Text Solution
|
- If a body is projected with a speed lesser than escape velocity, then
Text Solution
|
- An orbiting satellite will escape if
Text Solution
|
- In case of an orbiting satellite, if the radius of orbit is decreased
Text Solution
|
- If two satellites of different masses are revolving in the same orbit,...
Text Solution
|
- A double star is a system of two stars of masses m and 2m, rotating ab...
Text Solution
|
- Mark the correct statements.
Text Solution
|