Interference: The modification of intensity obtained by the super position of two (or) more light wave is called interference.
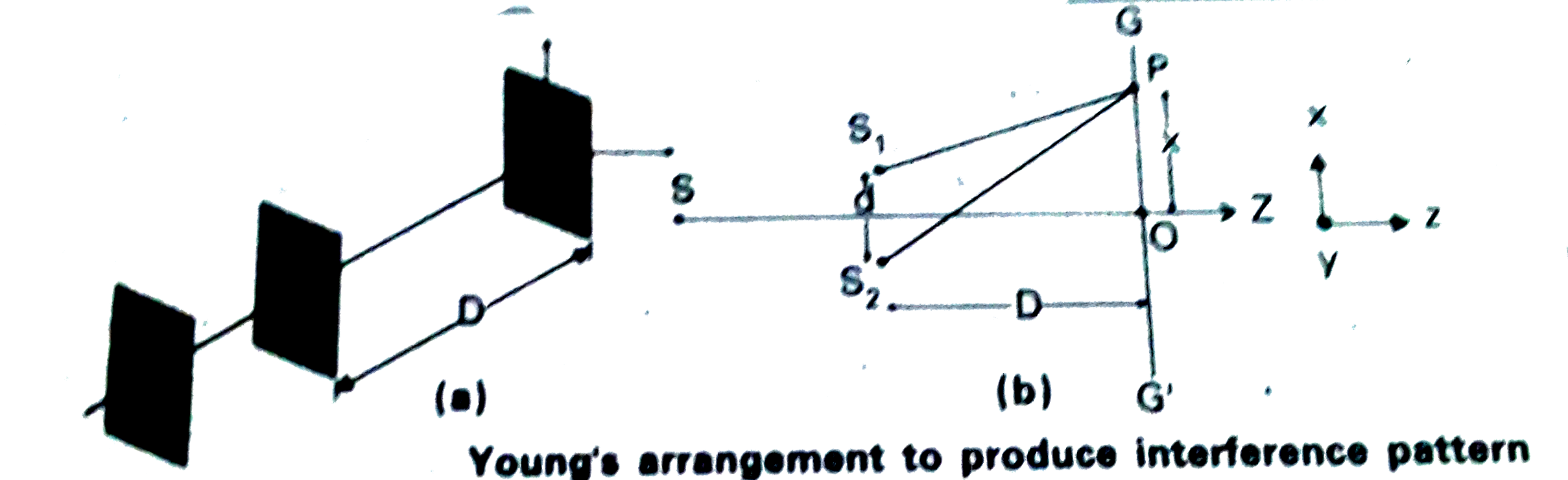
(i) Thomas Young experimentally observed the phenomenon of interference of light using two coherent sources.
(ii) A small pin hole 'S' illuminated by monochromatic source of light which produces a sphereical wave.
(iii) `S_(1) and S_(2)` are two narrow pin holes equidistant from S.
(iv) Screen is placed at a distance D.
(v) The points at which two crests (or ) any two troughts are superimposed, constructive interference takes place bright fringe will be observed on the screen.
(vi) The points at which crest of one wave and trought of another ave are super imposed, destructive interference takes place dark fringe will be observed on the screen.
(vii) Thus on the screen alternately bright and dark frings are observed.
Expression for fringe width:
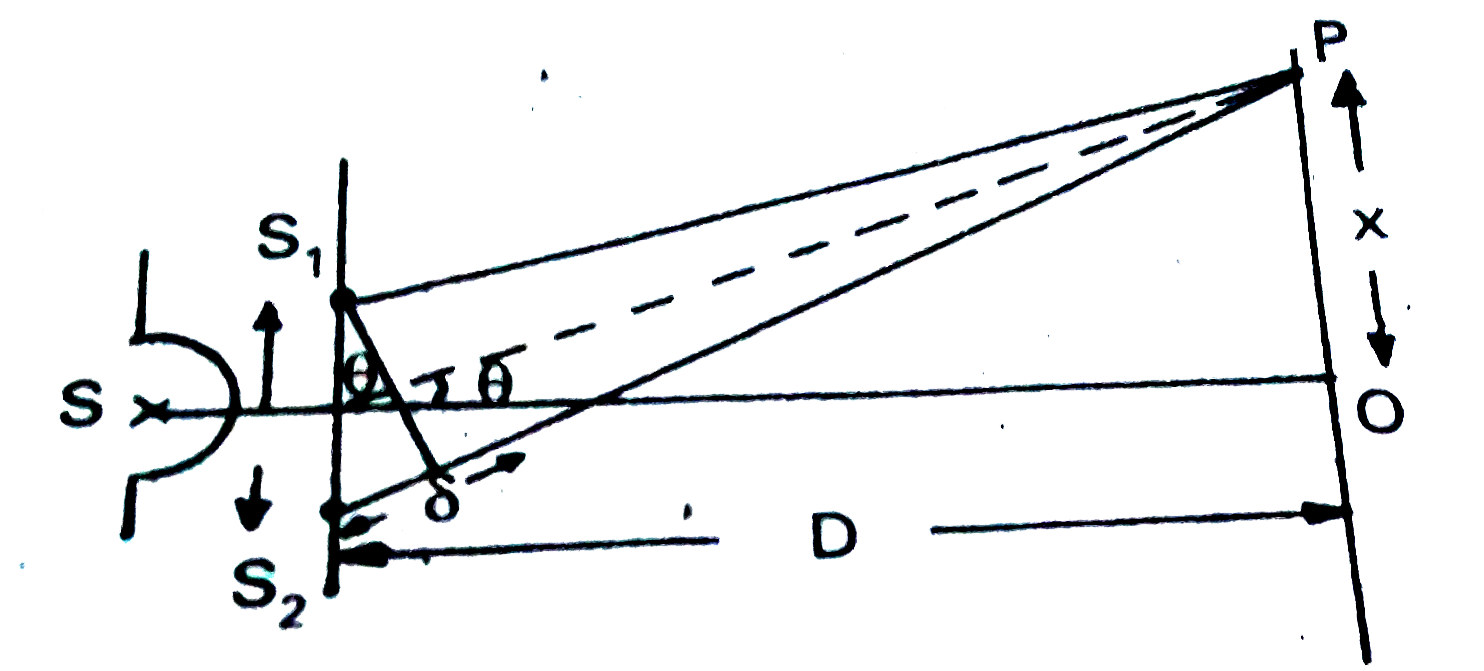
(i) It is the distance two sucessive bright (or) dark fringes, denoted by `beta`.
(ii) The path difference `(delta)=d sin theta`
If `theta` is very small then from figure `sin theta cong tan theta=(x)/D`
(iii) For bright frings path differences `S_(2)P-S_(1)P=nlambda`
`therefore d sin theta=nlamda`
`d xx x/D=nlambda`
`x=(nlambdaD)/(d)........(1)" where n"=0,1,2,3....`
This equation represents the position of bright fringe.
When, `n=0, x_(0)=0`
`n=1, x_(1)=(lambdaD)/d and n=2, x_(2)=(2lambdaD)/(d)`
The distance between any two consecutive bright fringe is `x_2-x_1=(2lambdaD)/(d)-(lambdaD)/(d) Rightarrow beta=(lambdaD)/(d).....(2)`
(iv) For dar fringes path differernce v`S_(2)P-S_(1)P=(2n+1)(lambda)/(2) therefore d sin theta=(2n+1)(lambda)/(2) d xx x/D=(2n+1) (lambda)/(2) Rightarrow x=((2n+1)lambdaD)/(2d) ......(3)" where n"=0,1,2,3,......`
This equation (3) represents, position of dar fringe
When `n=0, x_(0)=(lambdaD)/(2d )Rightarrow n=1, x_(1)=(3lambdaD)/(2d),n=2, x_(2)=(5lambdaD)/(2d)....`
The distance between any two consecutive dark fringes is `x_(2)-x_(1)=(5lambdaD)/(2d)-(3lambdaD)/(2d)=(5lambdaD-3lambdaD)/(2d) beta=(lambdD)/(d).....(4)`
Hence fringe width is same for bright and dark fringes.