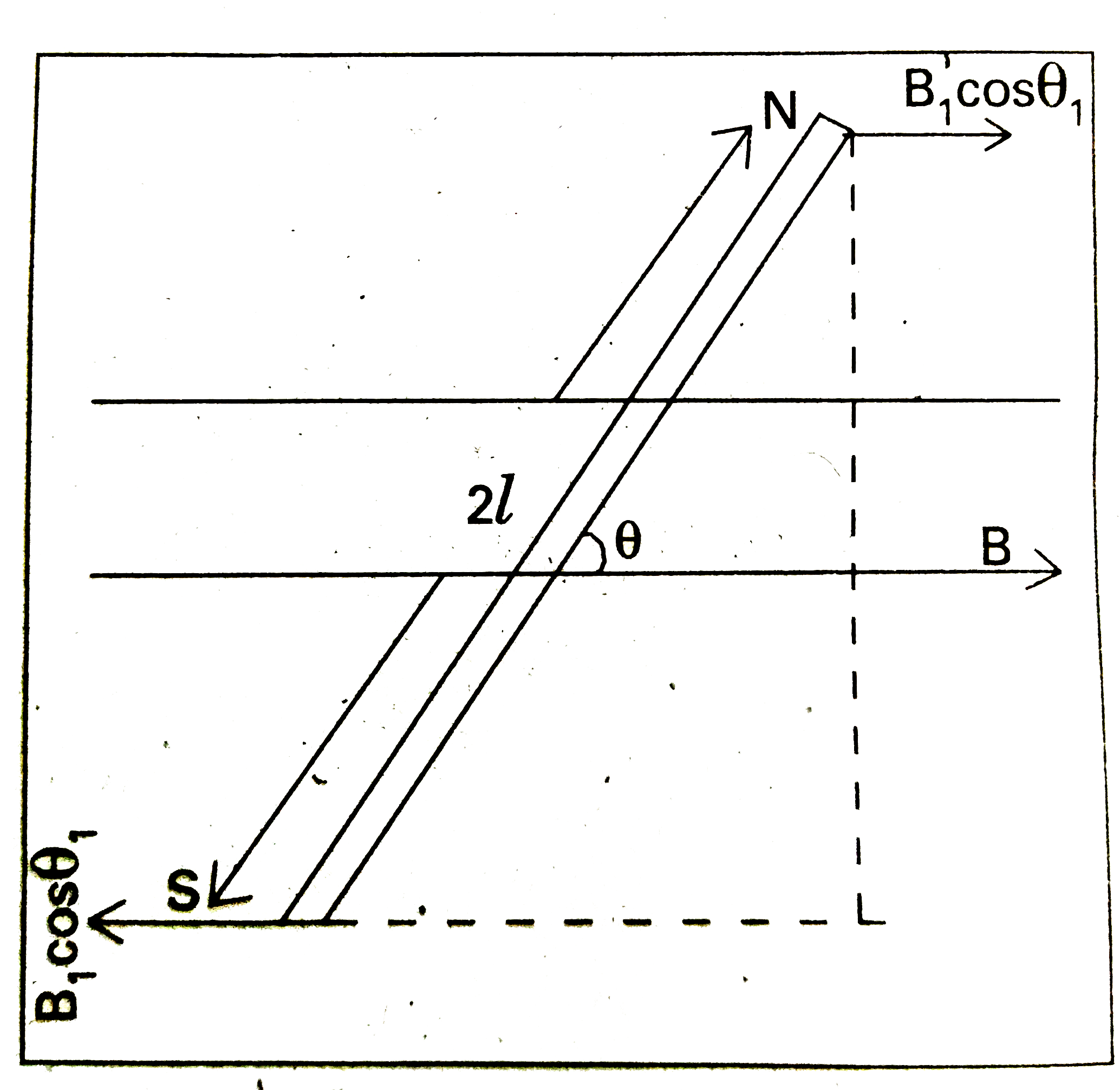
Text Solution
Verified by Experts
Topper's Solved these Questions
MAGNETISM AND MATTER
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Textual Exercises|27 VideosMAGNETISM AND MATTER
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Additional Exercises|19 VideosMAGNETISM AND MATTER
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Short Answer Questions|10 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise SAQs|4 VideosMOVING CHARGES AND MAGNETISHM
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise ADDITIONAL EXERCISES|26 Videos
Similar Questions
Explore conceptually related problems
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-MAGNETISM AND MATTER-Long Answer Questions
- Derive an expression for the magnetic field at a point on the axis of ...
Text Solution
|
- A small magnetic needle is set into oscillations in a magnetic field B...
Text Solution
|
- 4 bar magnet, held horizontally, is set into angular oscillations in t...
Text Solution
|
- Define magnetic susceptibility of a material. Name two elements one ha...
Text Solution
|
- Obtain Gauss'Law for magnetism and explain it.
Text Solution
|
- What do you understand by "hysterisis"? How does this property infulen...
Text Solution
|