Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-CAPACITOR AND CAPACITANCE-Integer
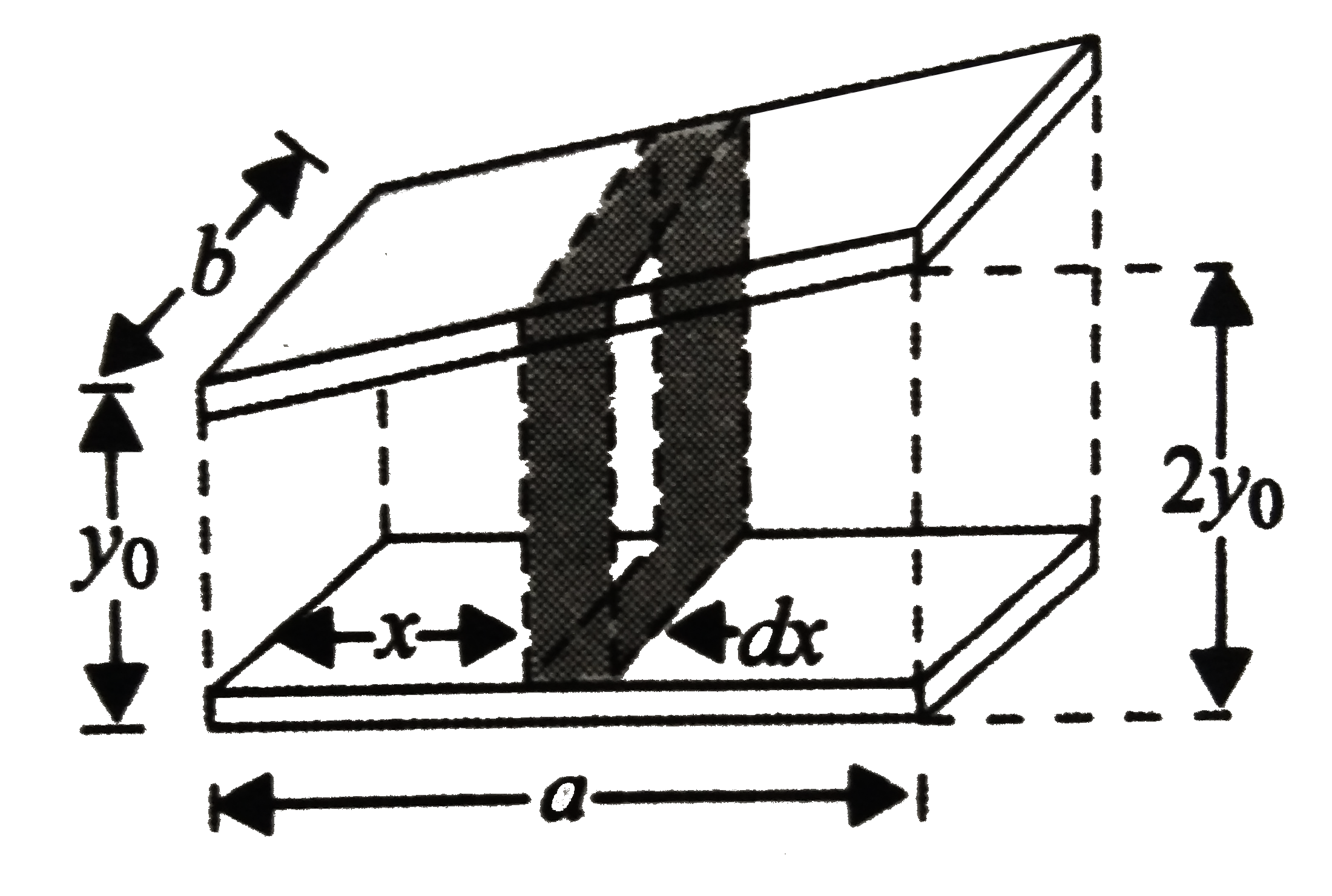
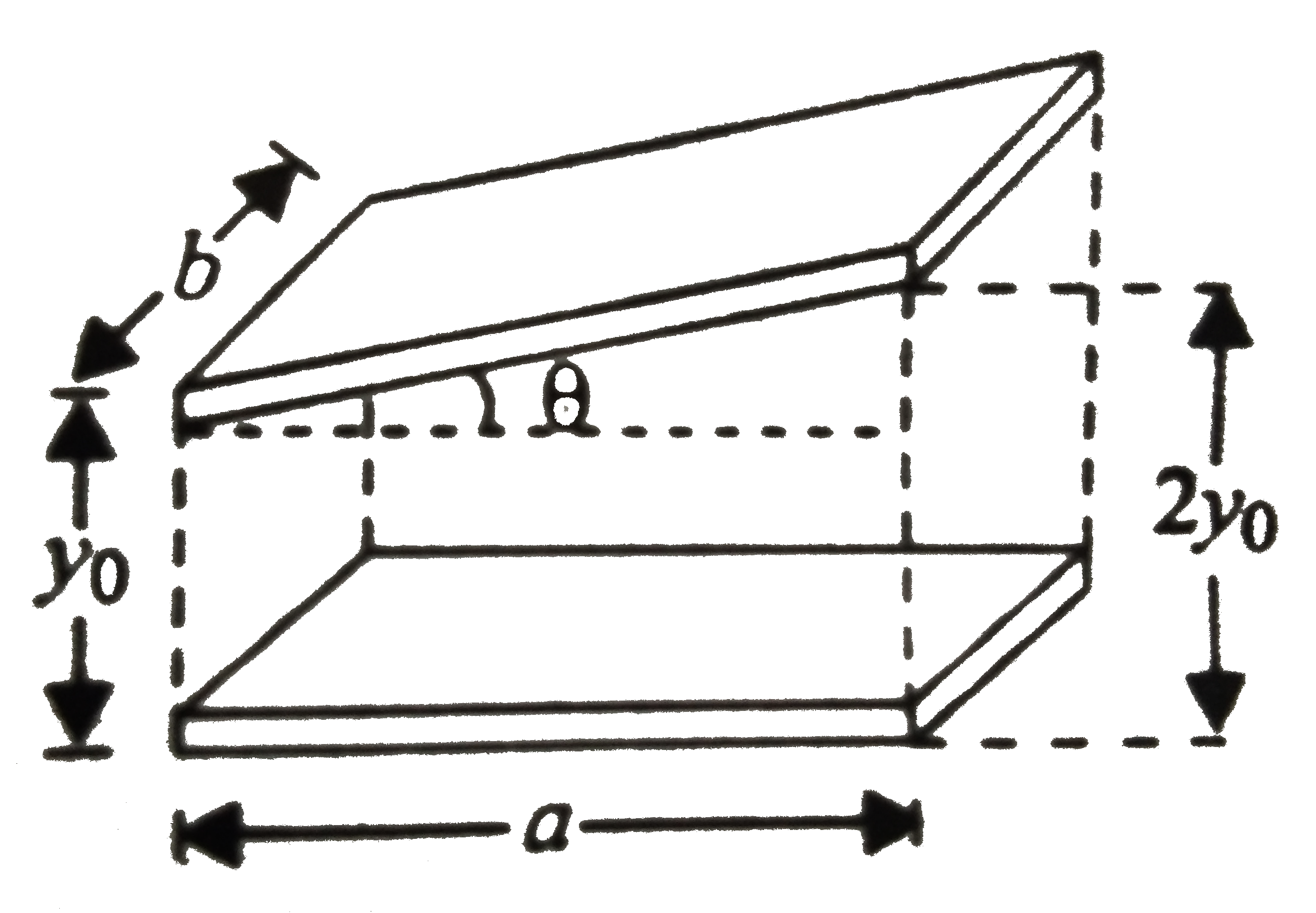
- A capacitor has rectangular plates of length a and width b. The top pl...
Text Solution
|
- Each capacitance shown in is in muF. Find the charge on 6 muC. .
Text Solution
|
- In, a potential of +12 V is given to point A, and point B is earthed. ...
Text Solution
|
- The capacitance of a capacitor becomes 4//3 times its original value i...
Text Solution
|
- A spherical drop of capacitance 12 muF is broken into eight drops of e...
Text Solution
|
- A parallel plate capacitor of capacity C(0) is charged to a potential ...
Text Solution
|
 .
.