Home
Class 12
PHYSICS
Three capacitors of capacitances 3 muF, ...

Three capacitors of capacitances `3 muF`, `6muF`, and `4 muF` are connected as shown across a battery of emg`6 V`. .
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.

Text Solution

Verified by Experts

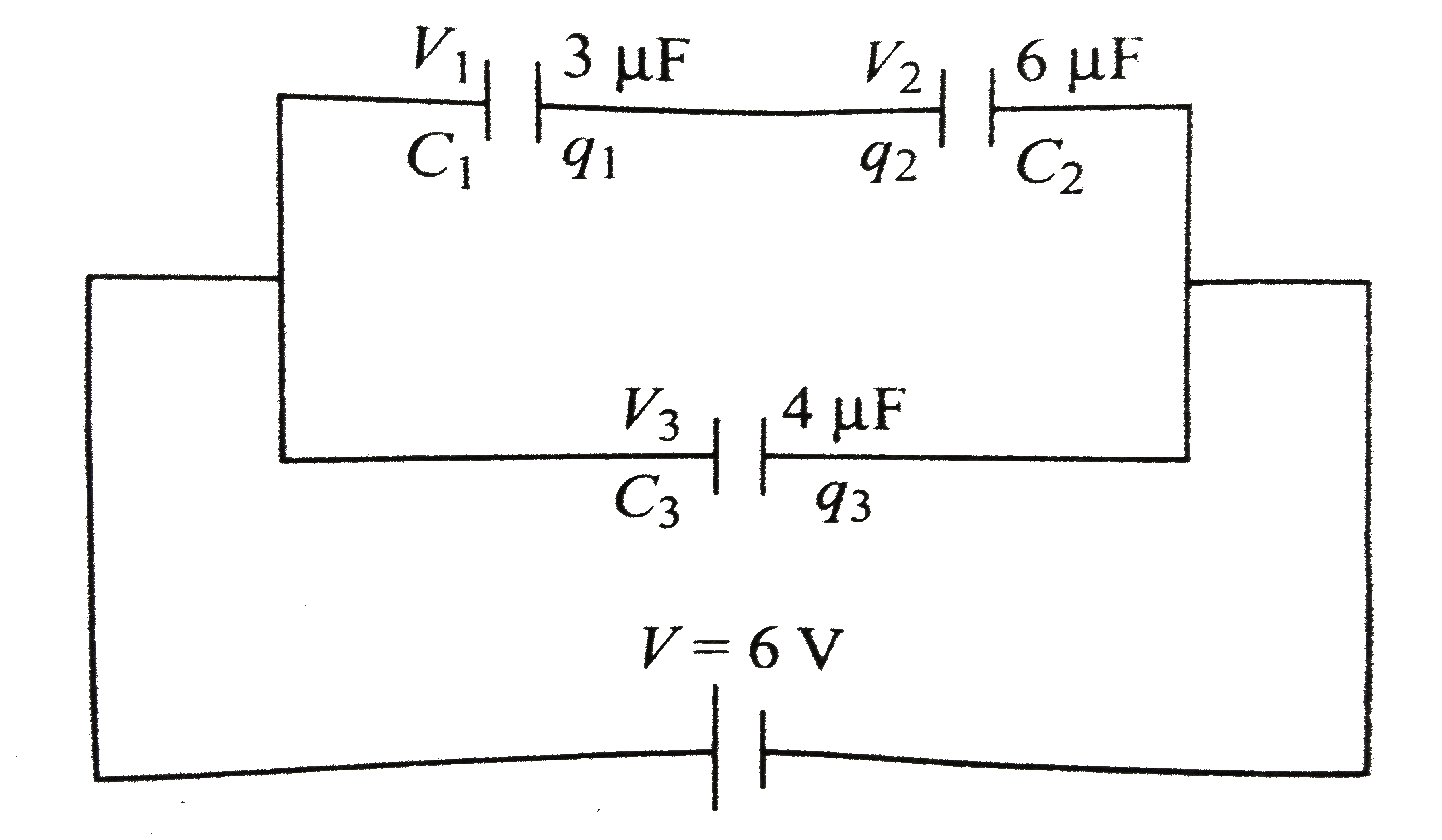
i. `C_(1)` and `C_(2)` are in series, so their equivalent capacitance is
`C=(C_(1)C_(2))/(C_(1)+C_(2))=(3xx6)/(3+6)=2 muF`
This `C'` will be in parallel `C_(3), So
`C_(eq)=C'+ C_(3)=2+4=6 muF`
ii. `6 V` will be in parallel across `C_(1)` and `C_(2)` in the inverse ratio of the capacitances. So potential defference across `C_(1)` is
`V_(1)=(C_(2)V)/(C_(1)+C_(2))=(6xx6)/(3+6)=4 V`.
and potential differnce across `C_(2)` is `V_(2)=(C_(1)V)/(C_(1)+C_(2))=(3xx6)/(3+6)=2 V`
Because `C_(3)` is connected directly aross the battery without any other capacitor in between , so potential difference across `C_(3)` is `V_(3) =V=6 V`. Also charge on `C_(1)` is
`q_(1)=C_(1)V_(1)=3xx4=12 muC`
and charge on `C_(2)` is
`1q_(2)=C_(2)V_(2)=6xx2-12 muC`
We see that `q_(1)q_(2)`, because is series, charge is the same.
chaege on `C_(3)` is
`q_(3)=C_(3)V_(3)=4xx6=24 muC`.
Alternative methode to find charge.

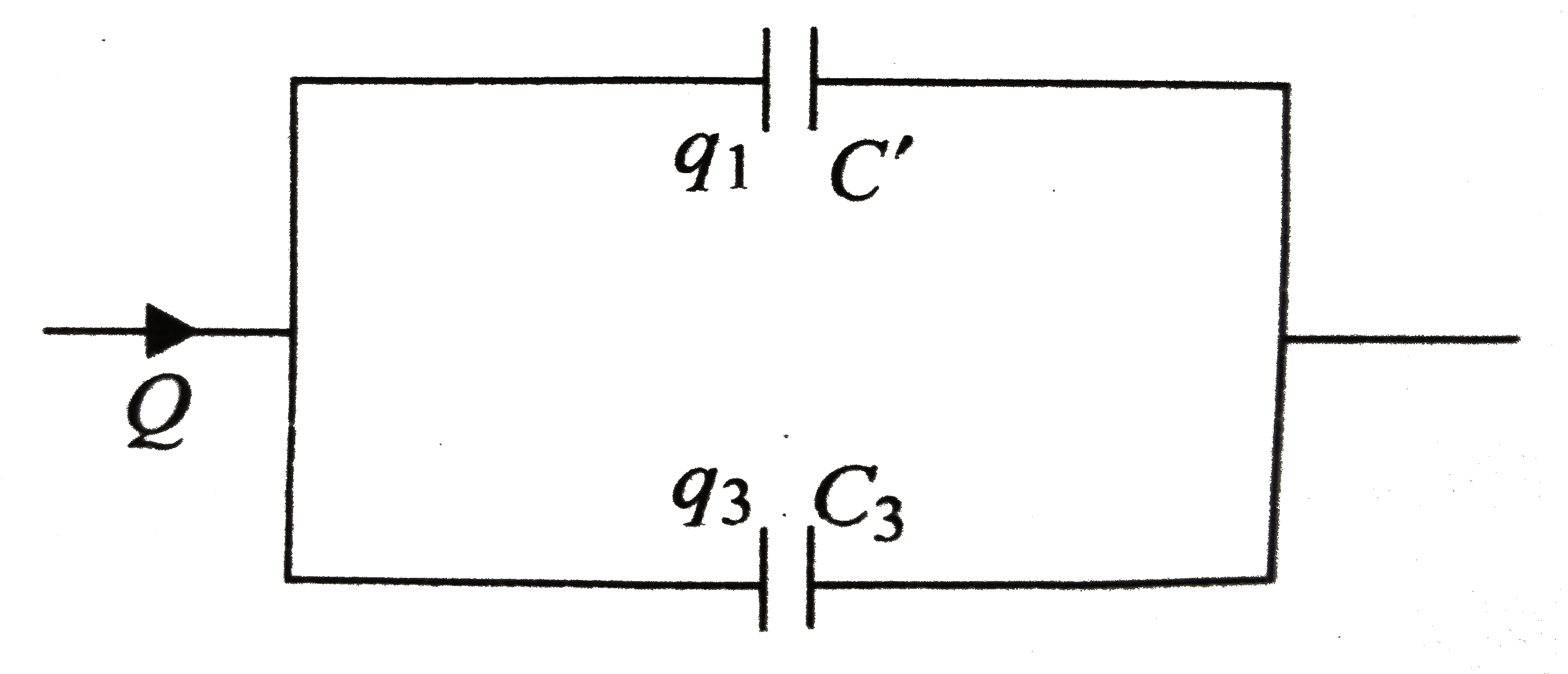
Total charge that will flow through the battery is
`Q = C_(eq)V = 6 xx 6 = 36 muC`
It will be divided inthe direct ratio of `C'` and `C_(3)`, so
`q_(1) = (C'Q)/(C'+C_(3)) = (2 xx 36)/(2+4) = 12 muC`
`q_(3) = (C'Q)/(C'+C_(3)) = (4 xx 36)/(2+4) = 24 muC`
Energy in `C_(1)` is
`U_(1) = (1)/(2)C_(1)V_(1)^(2) = (1)/(2)xx3xx4 = 24mu J`
Energy in `C_(2)` is
`U_(2) = (1)/(2)C_(2)V_(2)^(2) = (1)/(2)xx6xx2^(2) = 12mu J`
Energy is `C_(3)` is
`U_(3) = (1)/(2)C_(3)V_(3)^(2) = (1)/(2)xx4xx6 = 72mu J`
Total energy is
`U = U_(1) + U_(2) + U_(3) = 24 + 12 + 72 = 108 mu J`
Alternatively
`U = (1)/(2) xx 6 xx 6^(2) = 108 muJ`
Promotional Banner

Topper's Solved these Questions

  • CAPACITOR AND CAPACITANCE

    CENGAGE PHYSICS|Exercise Solved Examples|10 Videos

  • CAPACITOR AND CAPACITANCE

    CENGAGE PHYSICS|Exercise Exercise 4.1|13 Videos

  • ATOMS

    CENGAGE PHYSICS|Exercise QUESTION BANK|40 Videos

  • CENGAGE PHYSICS DPP

    CENGAGE PHYSICS|Exercise subjective type|51 Videos

Similar Questions

Explore conceptually related problems

Three capcitors of capacitances 4 muF , . 4 muF , and 8 muF , are connected as show across a battery of emf 12 V . i. Find the equivalent capacitane. ii. Find the potential difference and charge on each capacitor. iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.

Two capacitors of capacitances C_1 = 6muF and C_2 = 3muF are connected in series across a cell of emf 18 V. Calculate (i) the equivalent capacitance, (ii) the potential difference across each capacitor, (iii) the charge on each capacitor.

Three capacitors of capacitance 1 muF, 2muF and 3 muF are connected in series and a potential difference of 11 V is applied across the combination. Then, the potential difference across the plates of 1 muF capacitor is

If a 4muF capacitor is charged to 1 kV, then energy stored in the capacitor is

Two capacitors of capacitances 4muF and 6muF are connected in series with a battery of 20 V. find the energy supplied by the battery.

Three capacitors of capacitances 2muF, 2muF and 4muF are connected across a battery of 10V as shown in the adjoining figure (g). Calculate the effective capacitance and charge on each capacitor.

Three capacitors of capacitances 2muF, 2muF and 4muF are connected to a battery of 10V as shown in the figure. Calculate the effective capacitance of the circuit and charge on each capacitor.

Four capacitors of capacitances 2 muF and 1muF are connected across a battery of 10V as shown in the figure (q). Calculate the net capacitance of the combination and net charge across each capacitor.

In the circuit shown in figure find a. the equivalent capacitance b. the charge stored in each capacitor and c. the potential difference across each capacitor.