Let the potential difference across the battery terminals be `V`
and the charge supplied be `Q`. We have to find the capacitance of a capacitor that would have the same charge `Q` on its plates as the battery at voltage `V`. Hence,
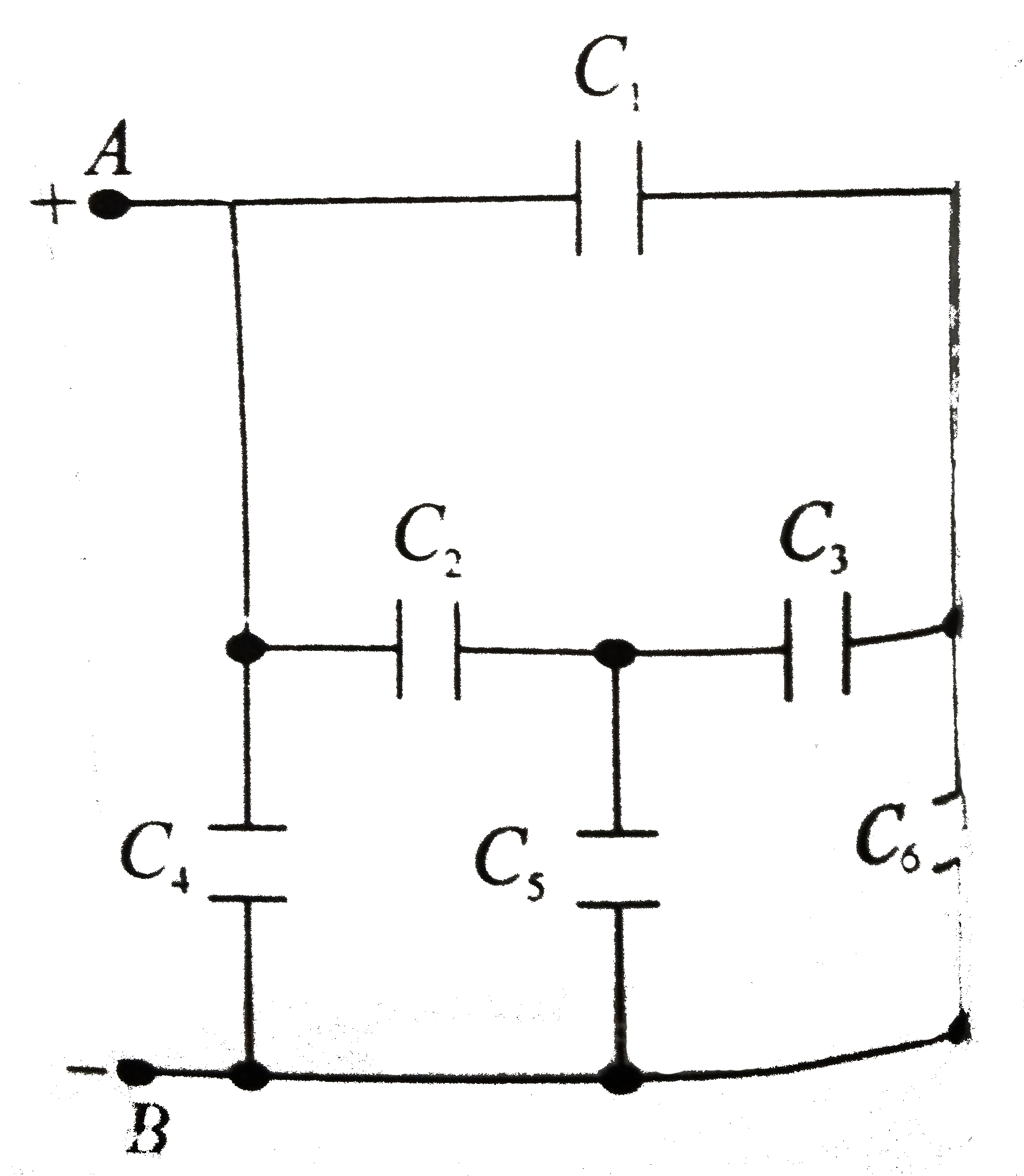
`C_("equivalent")=Q/(V_(A)-V)+_(B)=Q/V`
The incoming charge `Q` is equal
to the charge recived by the plates of the capacitors `C_(1),C_(2)` and `C_(4)`. Thus,
`Q=q_(1)+q_(2)+q_(4)`

.
Similarly outgoing charge `Q` is equal , to charge coming out from the plates of the capacitors `C_(4), C_(5)` and `C_(6)`.
`Q=q_(4) +q_(5)+q_(6)`
The above equations give
`q_(1) +q_(2)=q_(5)+q_(6)`
In a closed loop, the net potential drop must be zero , according to Kirchhoff's voltage law. Therefore, for loop `(1)`, loop `(2)`, and loop `(3)`, we have
(1) `q_(1)/C-q_(2)/C-q_(3)/C=0 rArr {:(q_1 = q_2 +q_3),(q_1 + q_2 = 2q_2 +q_3):}]` (ii)
(2) `q_(2)/C-q_(4)/C+q_(5)/C=0 rArr q_(4)=q_(2)+q_(5)` (iii)
(3) `q_(3)/C-q_(5)/C-q_(6)/C=0 rArr {:(q_5 = q_3 +q_6),(q_5 + q_6 = 2q_6 +q_5):}}` (iv)
From the isolated system shown in. we can conclude
`q_(3)+q_(5)-q_(2)=0` (v)
From Eqs. `(i), (ii`), and `(iv)`, we conclude `q_(2) = q_(6)` and `q_(1) = q_(5)`.
If `q_(1) = q_(5)`, then Eq. `(v)` becomes
`q_(2) - q_(1) = q_(3)` (vi)
Solving Eqs. `(ii)` and `(vi)`, we get
`q_(3) = 0, q_(1) = q_(2) = q_(5) = q_(6) = (q_(4))/(2)`, and `Q = 2q_(4)`
We can write
`V=(q_(4))/C` or `Q/V=2C`
Hence,
`C_("equialent")=Q/(V_(A)-V_(B))=Q/V=2C`.
Alterative method: Connect point `a` to point `b` note the inddicated Wheatstone bridge. Now simplify circute to obtain the desired result.
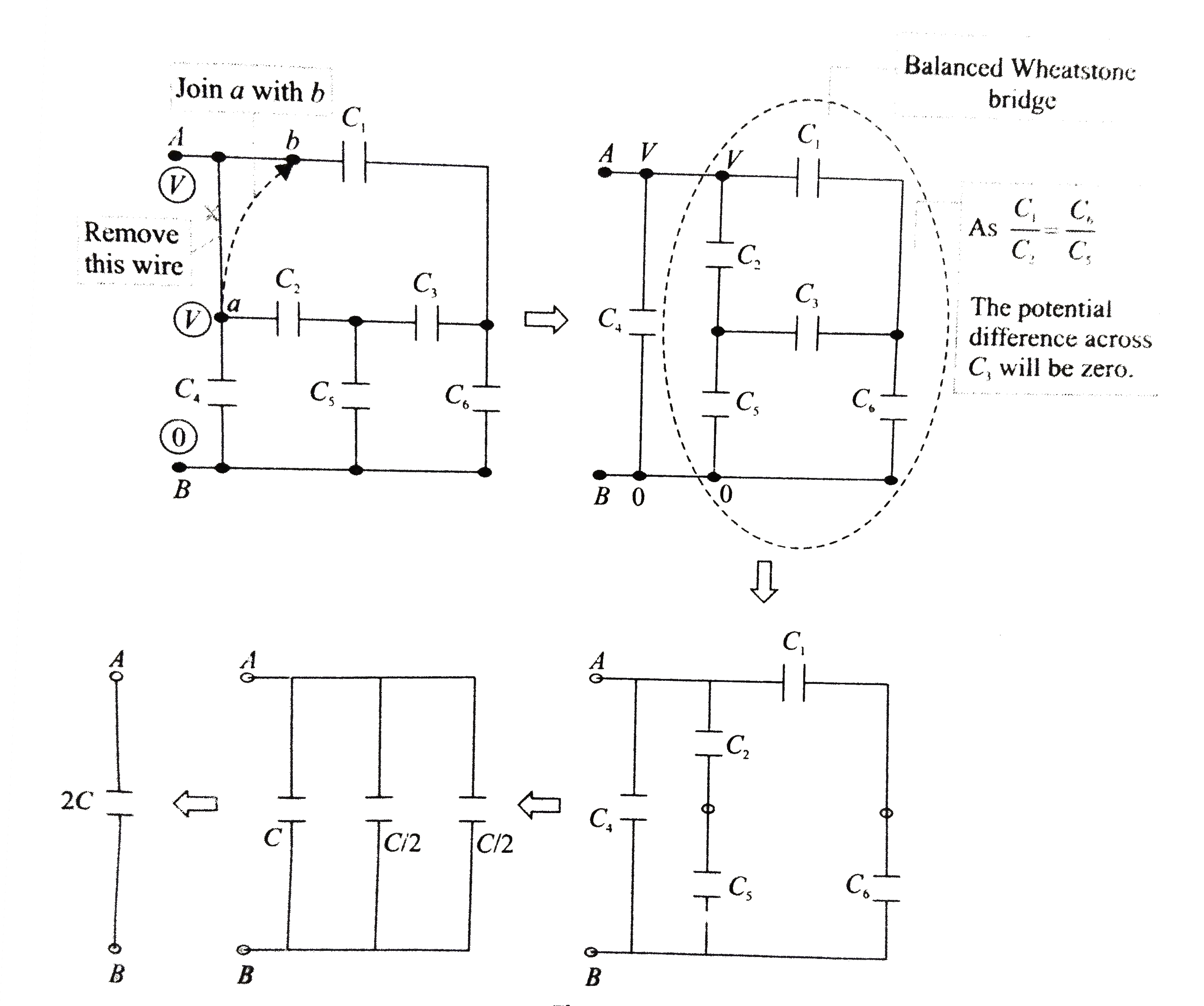

 .
. 