As the potentials of a and c are equal, the capacitors `C_(ab)` and `C_(bc)` are in parallel. Therefore,
`C_(ab)=C_(bc)=(epsilon_(0)A)/d =(epsilon_(0)xx2xx10^(-2))/(0.2xx10^(-3)) = 100 epsilon_(0)(F)`
Equivalent capacitance is
`C=C_(ab)+C_(bc)=(2epsilon_(0)A)/d`
`=(2xxepsilonxx2xx10^(-2))/(0.2xx10^(-3))=200epsilon_(0)(C)`
The charge on plat b is negetive on both faces. Thus, the charge on faces a and c is
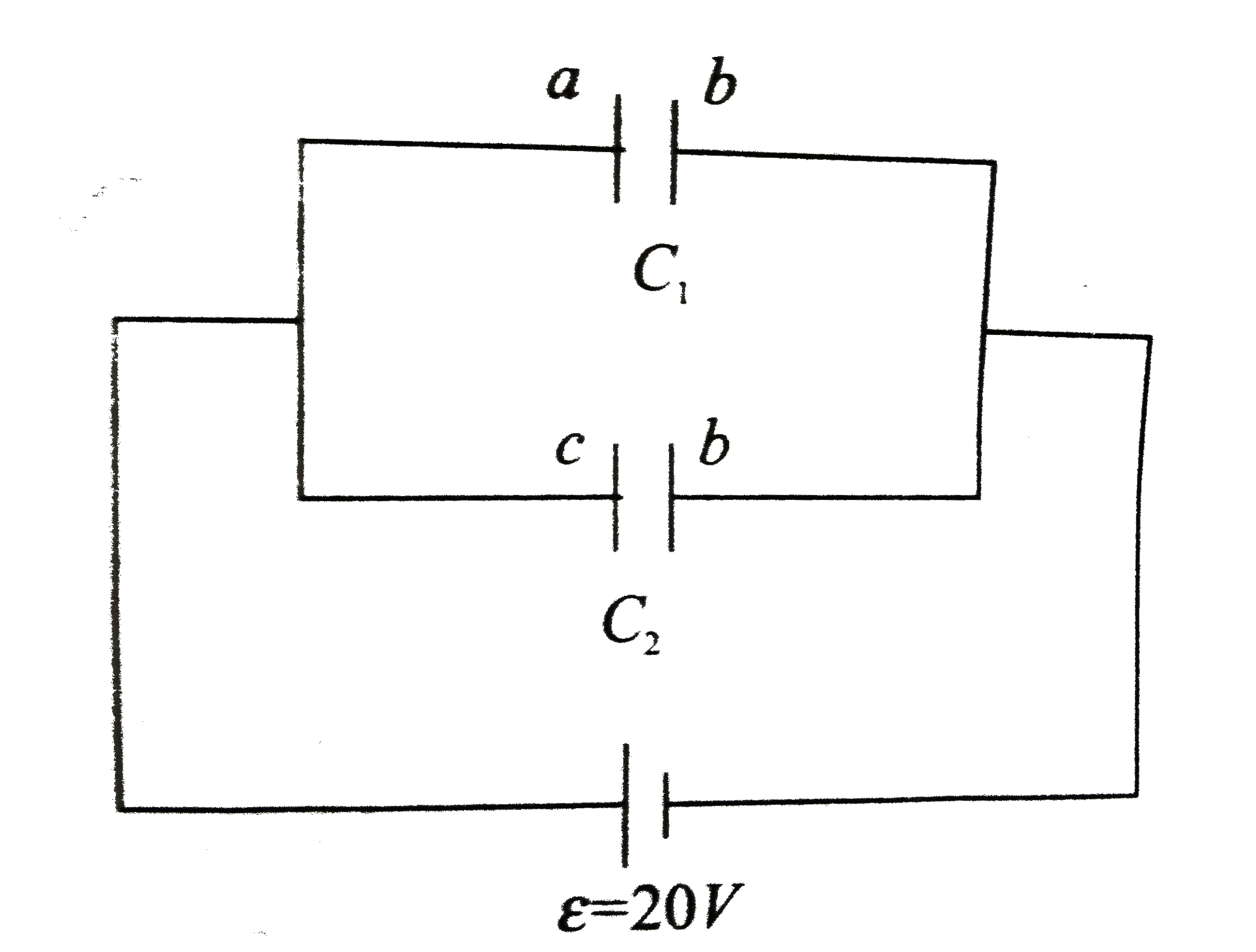
.
`q_(a)=q_(c)=(epsilon_(0)A)/(d)epsilon`
`=100 epsilon_(0)xx20`
`=2000epsilon_(0)(C)`
`:. Q=2xx2000epsilon_(0)(C)`
`=4000epsilon_(0)(C)`
Alternative method : Let us assume that the potential of the middle plate be zero, Then the potential of the left and right plates will be `20 V` each. Let the positive terminal of the battery lupply a charge `Q` . This charge is divided into two plates as shown in. The charge on the outermost surfaces will be zero,

.
Equal and opposite charges will appear on both surfaces of the mid plate (pate2).The sum of the charges on both the surfaces should be `-Q`, which will flow toward the negative terminal of the battery. we can observe two capacitors `C_(1)` and `C_(2)` for capacitor `C_(1)`
`x=C(20-0)` (i)
For capacitor `C_(2)`
`(Q-x)=C(20-0)` (ii)
From (i)
`x=(epsilon_(0)A)/(d)xx20=(epsilon_(0)(2xx10^(-2)))/(0.2xx10^(-3))xx20=2000epsilon_(0)(C)`
Also from (ii)
`(Q-x)=2000epsilon_(0)(C)`
The net charge on the mid plate is
`-x+(Q-x)=-2xx2000epsilon_(0)=-4000epsilon_(0)(C)`
Hence, the equivalent capacity is
`C_(eq)=Q/(epsilon)=(4000epsilon_(0))/(20)`
or `C_(eq)=200epsilon_(0)(F)`.

 .
.  .
.