Home
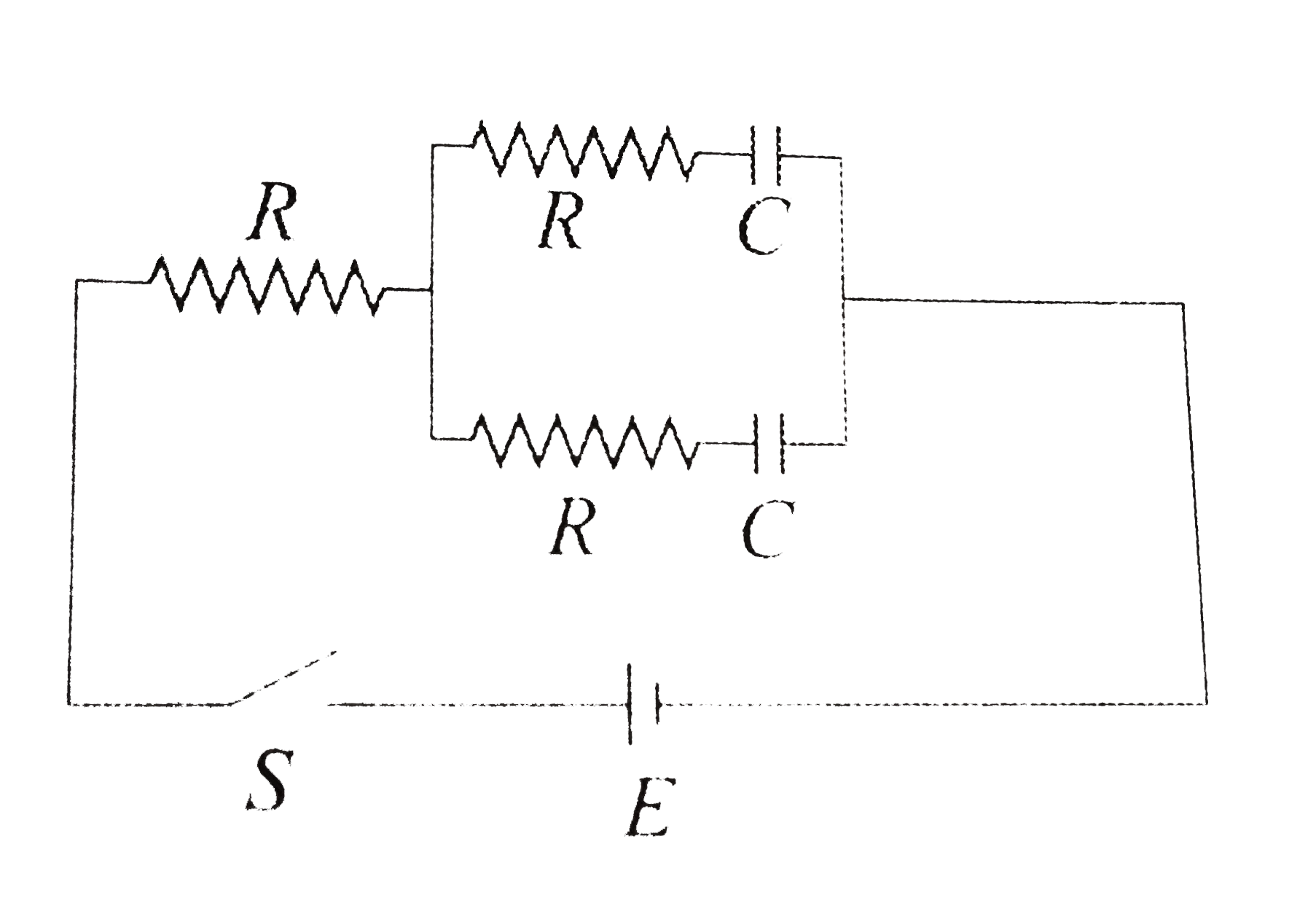
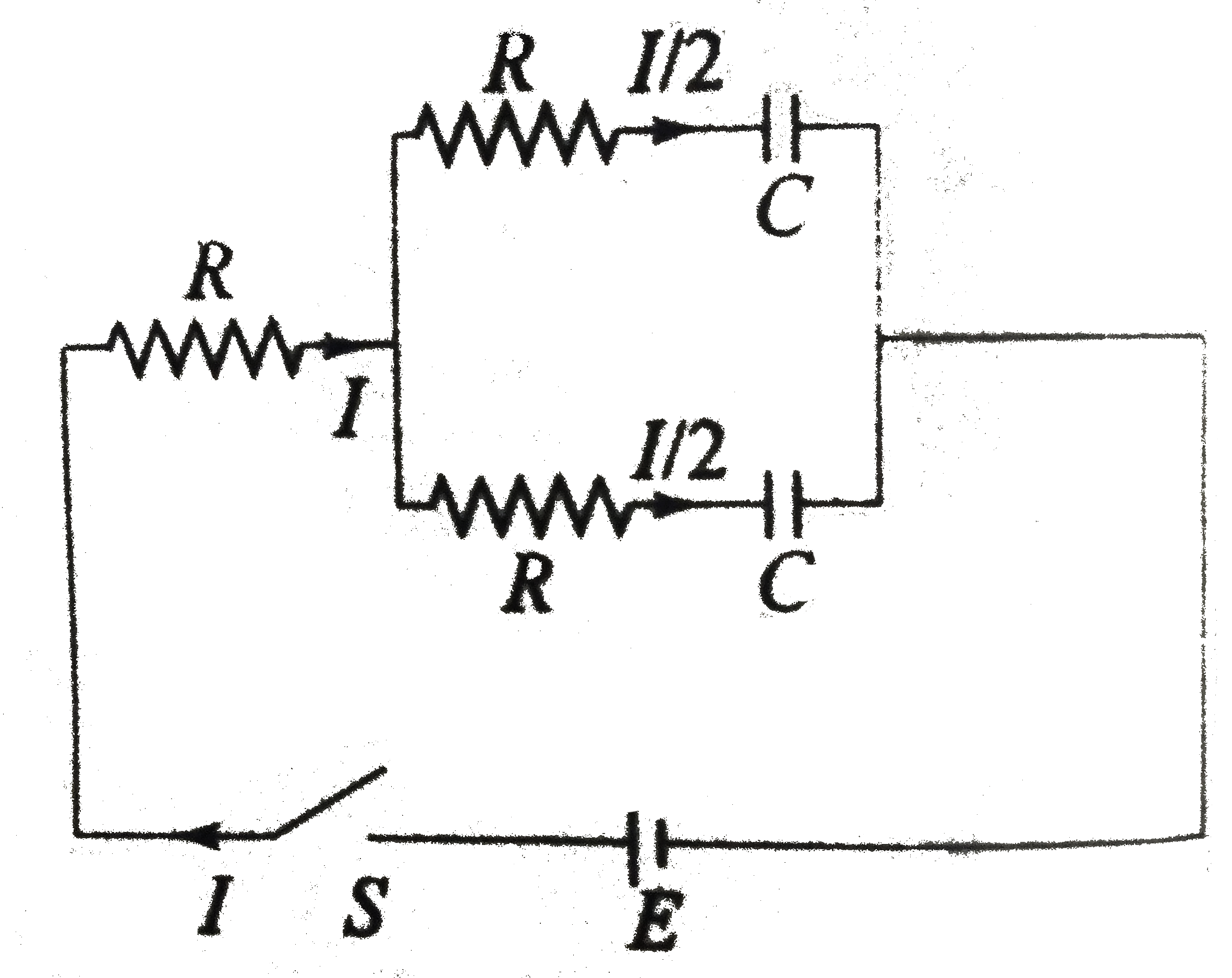Class 12
PHYSICS
The switch S in the circuit diagram is c...

The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is

A

`q_(t) = EC(1-e^(-2t//3RC))`

B

`q_(t) = EC(1-e^(-t//2RC))`

C

`q_(t) = EC(1-e^(-t//3RC))`

D

`q_(t) = EC(1-e^(-3t//2RC))`

Text Solution

Verified by Experts

The correct Answer is:
C
c. Applying KVL, we get
`1/2 = (dq)/(dt) or I = 2 (dq)/(dt)`
`E - IR -1/2R - q/C = 0`
or `E -3/2 IR - q/C =0 `
or `E - 3/2 xx 2 (dq)/(dt) R - q/C = 0`
`q_(t) = EC(1-e^(-t//3RC))`.
Promotional Banner

Similar Questions

Explore conceptually related problems

The switch shown n the figure is closed at t=0 . The charge on the capacitor as a function of time is given by

In given circuit, switch S is closed at t=0 . The charge on the capacitor ar steady state will be

In the given circuit, the switch S is closed at time t = 0 . The charge Q on the capacitor at any instant t is given by Q(t) = Q(1-e^(-alphat)) . Find the value of Q_0 and alpha in terms of given parameters as shown in the circuit. .

In the following circuit, the switch S is closed at t = 0. The charge on the capacitor C_(1) as a function of time will be given by (C_(eq)=(C_(1)C_(2))/(C_(1)+C_(2)))

In the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 . (a) Find the charge Q on the capacitor at time t. (b) Find the current in AB at time t. What is its liniting value as t rarr oo : .

The switch S of the circuit is closed at t = 0. Find the current (in Amp.) through the capacitor when the switch S is closed at t = 0

In the circuit shown in figure-3.244, the battery is an ideal one with emf V. The capacitor is initially uncharged. The switch S is closed at time t=0. (a) Find the charge Q on the capacitor at time l (b) Find the current in branch AB at time just after closing the switch.

In the circuit shown, the capacitor C_1 is initially charged with charge q_0 . The switch S is closed at time t = 0 . The charge on C_2 after time t is

Consider two circuits given below. When switches S_(1) and S_(2) are closed at t = 0 , the charge on capacitors C_(1) and C_(2) change with time as shown in graph 1 and 2 respectively. The current i_(1) and i_(2) in the two circuits change as shown in graph 1' & 2' respectively. Write the variation of current in the second circuit as function of time after the switch is closed at t=0. e^(-1) =0.37