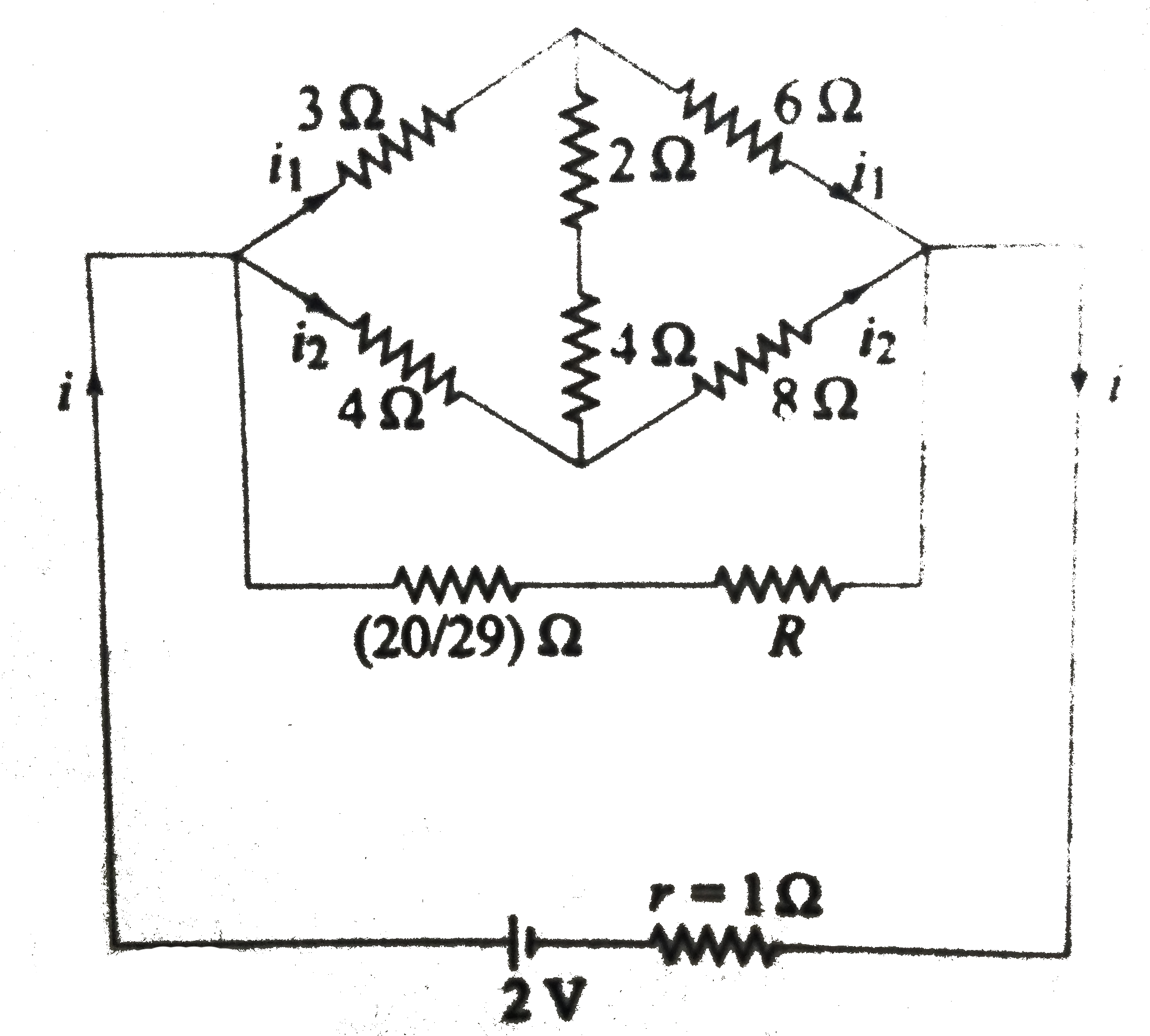
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A battery of emf 2 V and initial resistance 1 Omega is connected acr...
Text Solution
|
- A battery of emf 2 V and initial resistance 1 Omega is connected acros...
Text Solution
|
- When a resistance of 2 Omega is placed across the terminals of a batte...
Text Solution
|
- Four resistors are connected as shown in the figure. A 6 V battery of ...
Text Solution
|
- A 5 V battery of negligible internal resistance is connected across a...
Text Solution
|
- A 10 V cell of neglible internal resitsance is connected in parallel...
Text Solution
|
- A cell of emf 2.0 V and internal resistance 0.1 Omega is connected wit...
Text Solution
|
- A 10 V battery of negligible internal resistance is connected across a...
Text Solution
|
- A 10 V battery of negilgible internal resistance is connected across a...
Text Solution
|
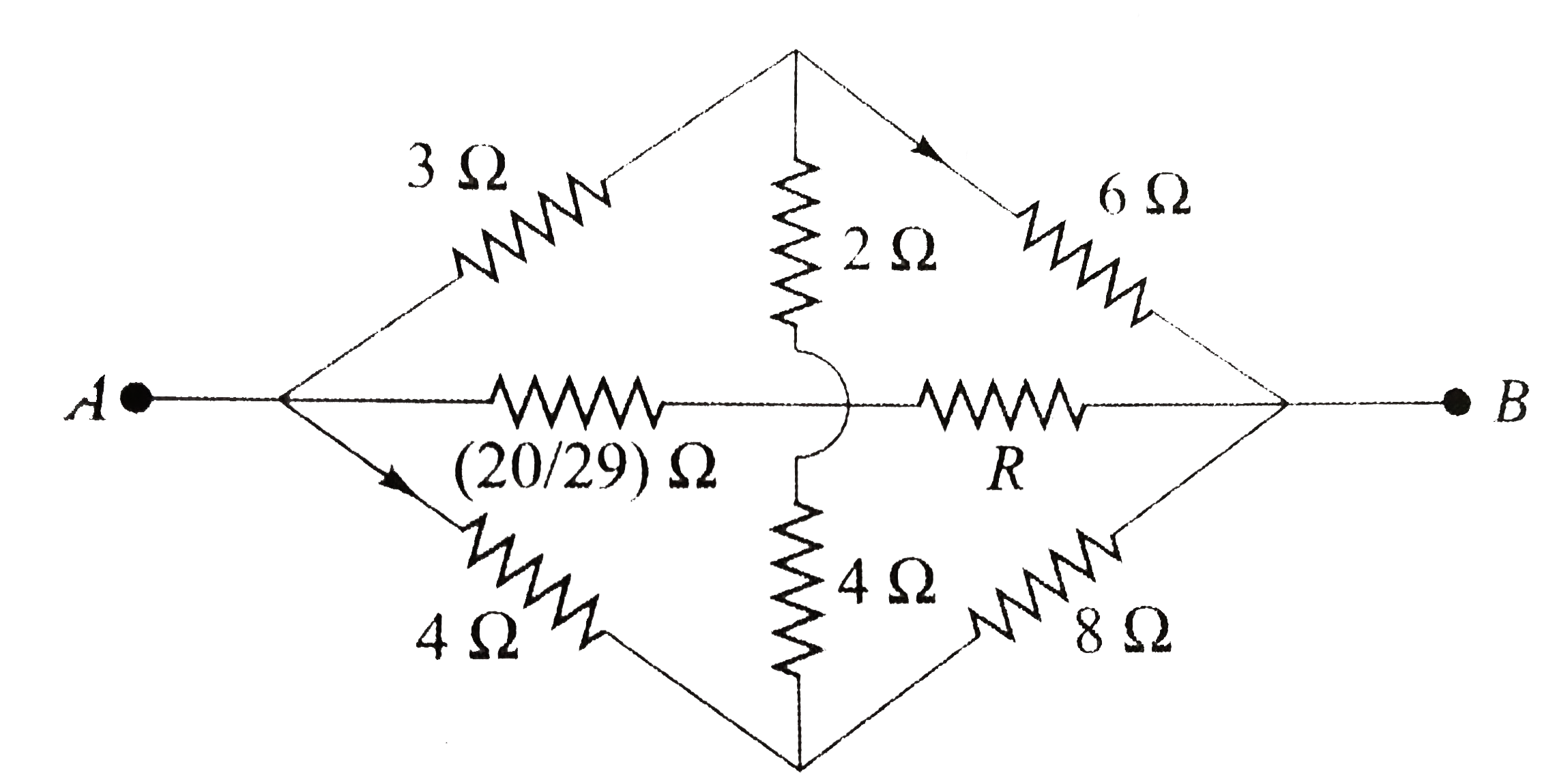 .
.