Consider the situation in Fig. The bottom of the pot is a reflecting plane mirror, S is a small fish, and T is a human eye. Refractive index of water is `mu`.
a. At what distance(s) from itself will the fish see the image(s) of the eye?
b. At what distance(s) from itself will the eye see the image(s) of the fish?

Explanation

a. The fish will observe the images of eye one from direct observation and the other reflected image from the plane mirror.
(i) Direct observation of eye from fish
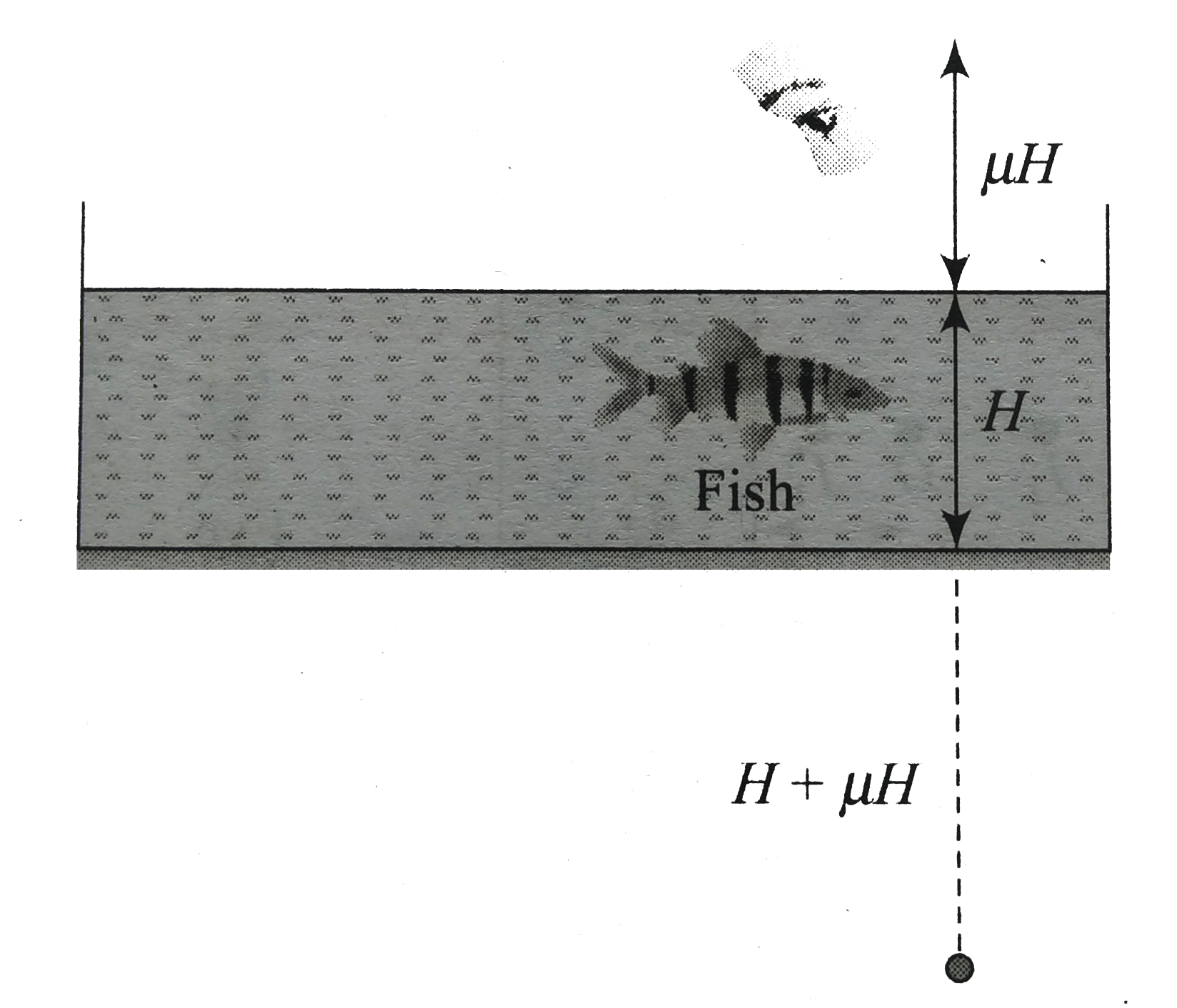
Apparent height, `H^'=H/n_("rel")=H/(n_("air")/n_("water"))=H/((1/mu))`
Hence, `H^'=muH`
Distance of image of eye from fish
`d=H/2+mu H=H(1/2+mu)`
(ii) Observation of reflected image of the eye from the fish
For mirror, the distance of eye from it will be `(H+ muH)`. Hence, the image of eye from mirror will be `(H+ muH)` behind the mirror. Hence, distance of image of eye from the fish
`d^(')=H/2+H+muH=3/2H+muH`
`rArr d^(') =H(3/2+mu)`
b. The eye will also observe two images of the fish, one from direct observation and the other reflected image from the mirror.
(i) Direct observation of fish from eye:
Apparent depth of the fish observed by the eye
`H^(')= (H//2)/n_(r)=(H//2)/((n_("water"))/n_(air))=(H//2)/mu=H/(2mu)` Distance of image of the fish from the eye,
`d=H+H/(2mu)=H(1+1/(2mu))`
(ii) Eye observing image of fish:
The eye will observe the image of fish reflected from the mirro.
Apparent depth of image of the fish from air and water interface.
`H^(')= (" Real depth ")/n_(" rel ")= (3/2H)/((n_("water")/n_("air")))`
Here real depth from top surface of water
`=H+H/2=3/2H`
`H^(')= (3H)/(2mu)`
Hence, distance between t his image and the eye,
`d^(')=H+(3H)/(2mu)=H+3(1+3/(2mu))`
,