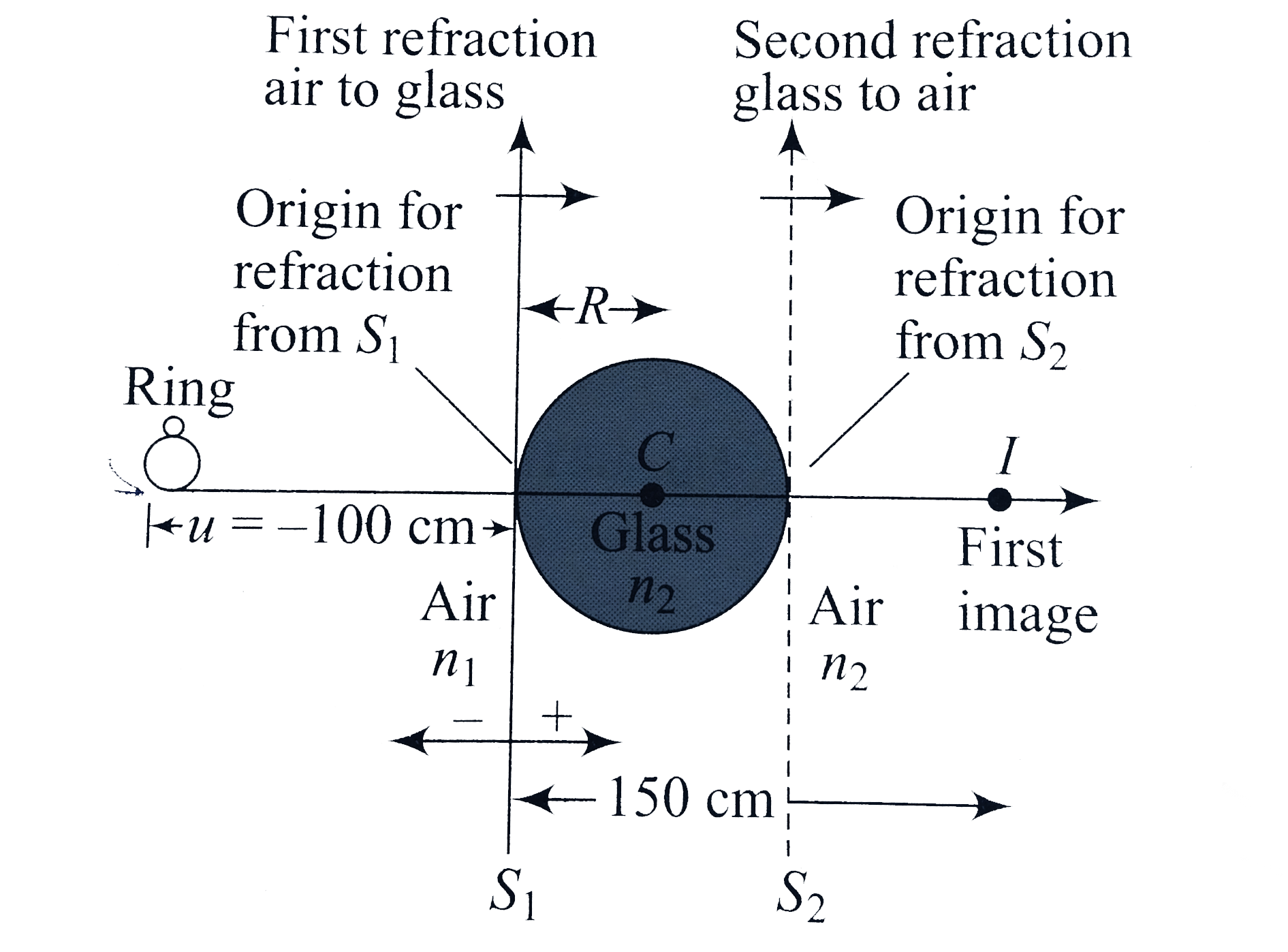
Light rays from the object are refracted through the glass ball twice, first at surface `S_(1)`, from air to glass, and second, at surface `S_(2)`, from the glass to air. We use paraxial approximation, so that single surface refraction equation can be used.
Refraction at first surface
`n_(1)=1, n_(2)=1.5, u=-100cm` , `R=+25cm`
The radius of curvature is positive because center of curvature is to the right.
Substitutinig these values in single surface refraction equation,
`(1.5)/(v)- (1)/((-100))=((1.5-1))/(2.5)`
On solving for v, we get `v =+150` cm
The image is located 150cm to the right of the first refracting surface. The magnification due to refraction at first surface,
`mu_(1)=(n_(1)v)/(n_(2)u)=(1(150))/(1.5(-100))=-1`
Refraction at second surface
For refraction at second surface, the origin of the cartesian coordinate system has to be shifted to the vertex of the second refracting surfac.
The object distance for refraction at `S_(2)` is
`u^(')=+(150-50)=100cm` .
This is the virtual object for `S_(2)`, the light rays converging to `I_(1)` are refracted at `S_(2)` before they can actually converge to form the image.
`n_(1)=1.5, n_(2)=1, u=100cm, R=-25cm`
`(1)/(v)-(1.5)/((+100))=((1-1.5))/((-25))rArr v=+200//7cm`
`mu_(2)=(n_(1)v)/(n_(2)u)=(1.5(200//7))/(1(100))=(3)/(7)`
`m=m_(1)xxm_(2)=-1xx(3)/(7)=-(3)/(7)`