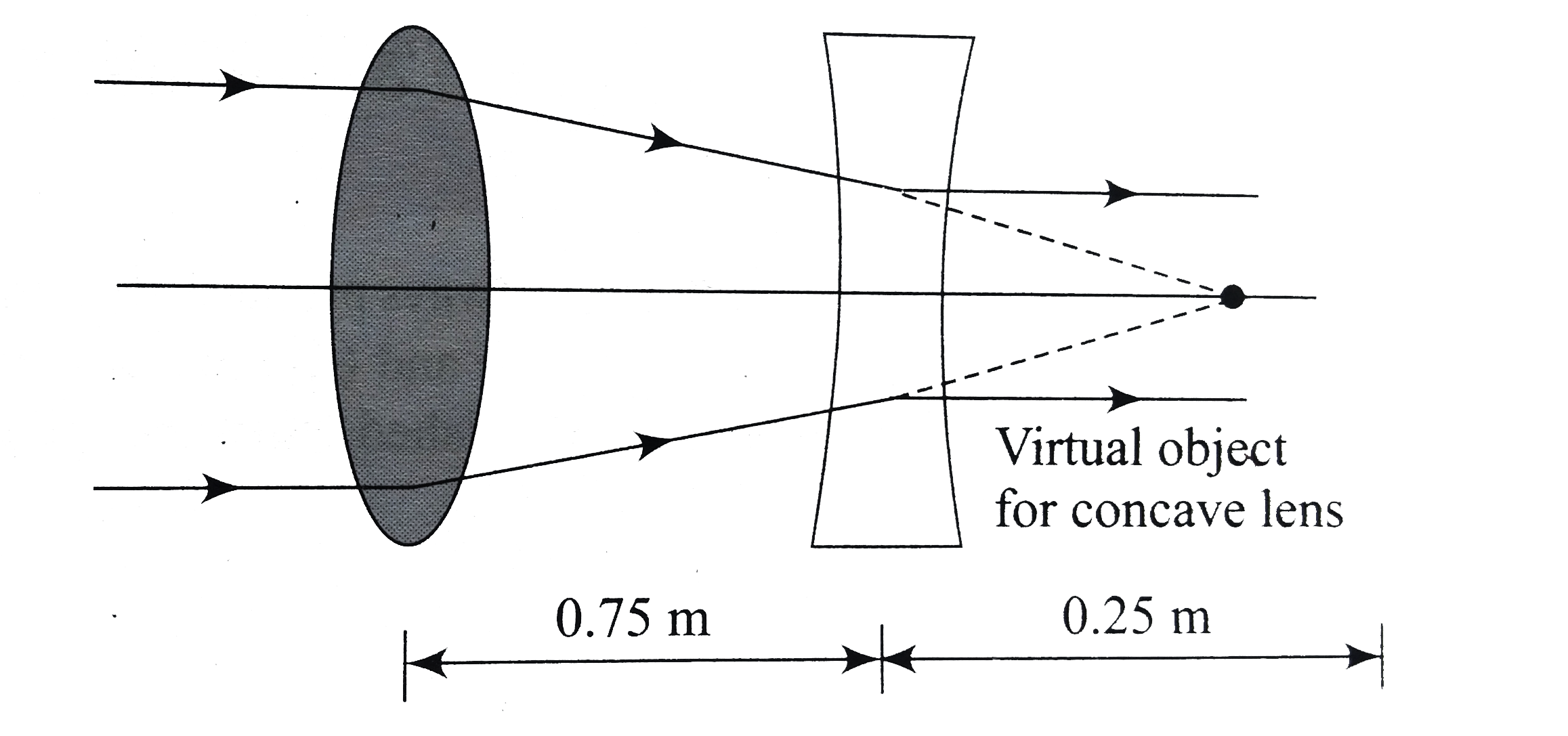
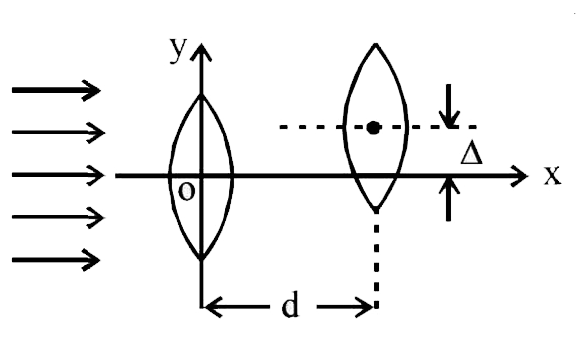A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GEOMETRICAL OPTICS
CENGAGE PHYSICS|Exercise Multiple Correct Answers Type|8 VideosGEOMETRICAL OPTICS
CENGAGE PHYSICS|Exercise Assertion-Reasoninig Type|2 VideosGEOMETRICAL OPTICS
CENGAGE PHYSICS|Exercise True/False|5 VideosFRICTION
CENGAGE PHYSICS|Exercise QUESTION BANK|1 VideosGRAVITATION
CENGAGE PHYSICS|Exercise Question Bank|39 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-GEOMETRICAL OPTICS-Single Correct Answer Type
- A beam of light consisting of red, green, and blue colors is incident ...
Text Solution
|
- A thin prism P(1) with angle 4degree and made from glass of refractive...
Text Solution
|
- Two thin convex lenses of focal lengths f(1) and f(2) are separated by...
Text Solution
|
- Spherical aberration in a thin lens can be reduced by
Text Solution
|
- A beam of light of wavelength 600nm from a distance source falls on a ...
Text Solution
|
- An isosceles prism of angle 120degree has a refractive index 1.44. Two...
Text Solution
|
- A diminished image of an object is to be obtained on a screen 1.0 m fr...
Text Solution
|
- The focal lengths of the objective and the eyepiece of a compound mic...
Text Solution
|
- An eye specialist prescribes spectacles having combination of convex l...
Text Solution
|
- Areal image of a distant object is formed by a plano-convex lens on it...
Text Solution
|
- A concave mirror is placed on a horizontal table, with its axis direc...
Text Solution
|
- A spherical surface of radius of curvature R separates air (refractive...
Text Solution
|
- A concave lens of glass, refractive index 1.5, has both surfaces of sa...
Text Solution
|
- A hollow double concave lens is made of very thin transparent material...
Text Solution
|
- A point source of light B is placed at a distance L in front of the ce...
Text Solution
|
- A diverging beam of light from a point source S having divergence ang...
Text Solution
|
- A rectangular glass slab ABCD of refractive index n(1) is immersed in ...
Text Solution
|
- In a compound microscope, the intermediate image is
Text Solution
|
- A ray of light passes through four transparent media with refractive i...
Text Solution
|
- A given ray of light suffers minimum deviation in an equilateral prism...
Text Solution
|