A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-WAVE OPTICS-Linked Comprehension
- In a YDSE perfromed with light of wavelength 600 Å, the screen is pla...
Text Solution
|
- In a YDSE perfromed with light of wavelength 600 Å, the screen is pla...
Text Solution
|
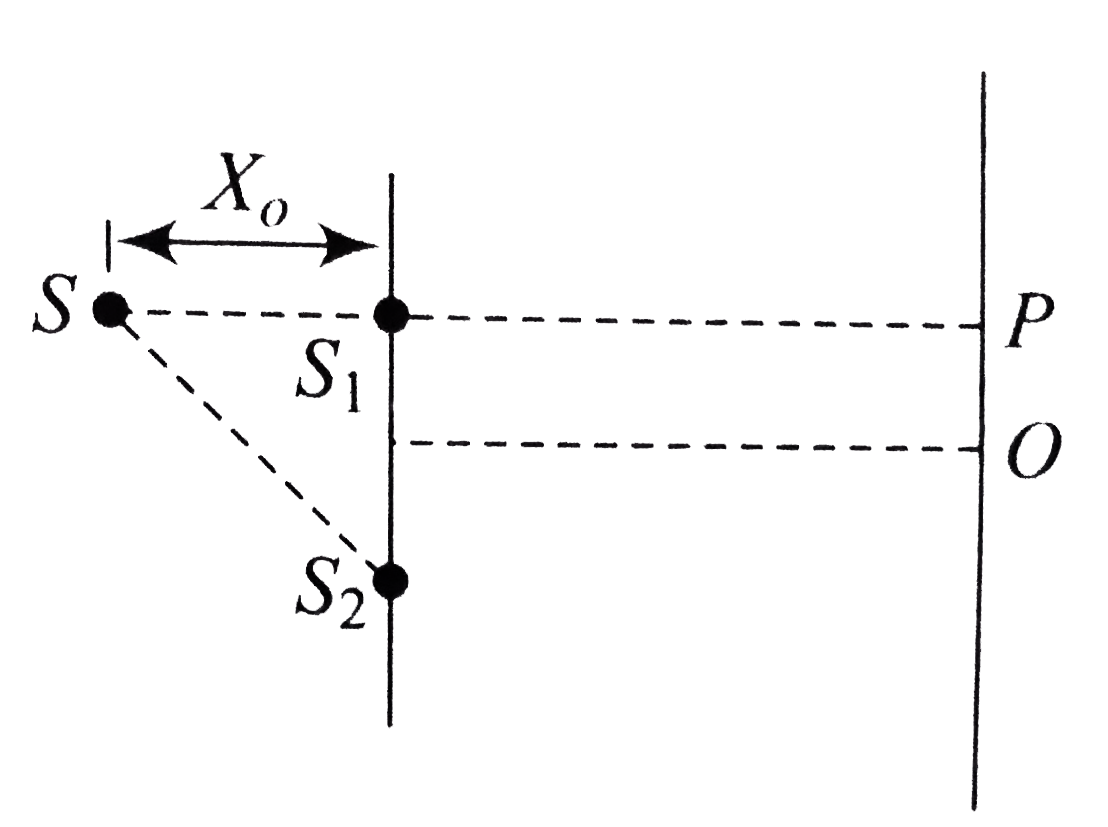
- In a modified YDSE, sources S is kept in front of slit S(1). Find the ...
Text Solution
|
- In a midified YDESE, sources S is kept in front of slit S(1). Find the...
Text Solution
|
- In a modified YDSE, the region between the screen and slits is immerse...
Text Solution
|
- In a modified YDSE, the region between the screen and slits is immerse...
Text Solution
|
- In a YDSE using monochromatic visible light, the distance between the ...
Text Solution
|
- In a YDSE using monochromatic visible light, the distance between the ...
Text Solution
|
- In figure, a screen is placed normaol to the line joining the two poin...
Text Solution
|
- In figure, a screen is placed normal to the line joining the two point...
Text Solution
|
- In figure, a screen is placed normaol to the line joining the two poin...
Text Solution
|
- In the arrangement shown in figure, light of wavelength 6000 Å is inci...
Text Solution
|
- In the arrangement shown in figure, light of wavelength 6000 Å is inci...
Text Solution
|
- A lens of focal length f is cut along the diameter into two identical ...
Text Solution
|
- A lens of focal length f is cut along the diameter into two identical ...
Text Solution
|
- In the arrangment shown in fin. For what minimum value of d is th...
Text Solution
|
- In the arrangment shown in fin. Find the distance x at which the n...
Text Solution
|
- In the arrangment shown in fin. Find the fringe width.
Text Solution
|
- Consider the situation shown in fig. The two slits S(1) and S(2) place...
Text Solution
|
- Consider the situation shown in fig. The two slits S(1) and S(2) place...
Text Solution
|