Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-NUCLEAR PHYSICS-ddp.5.5
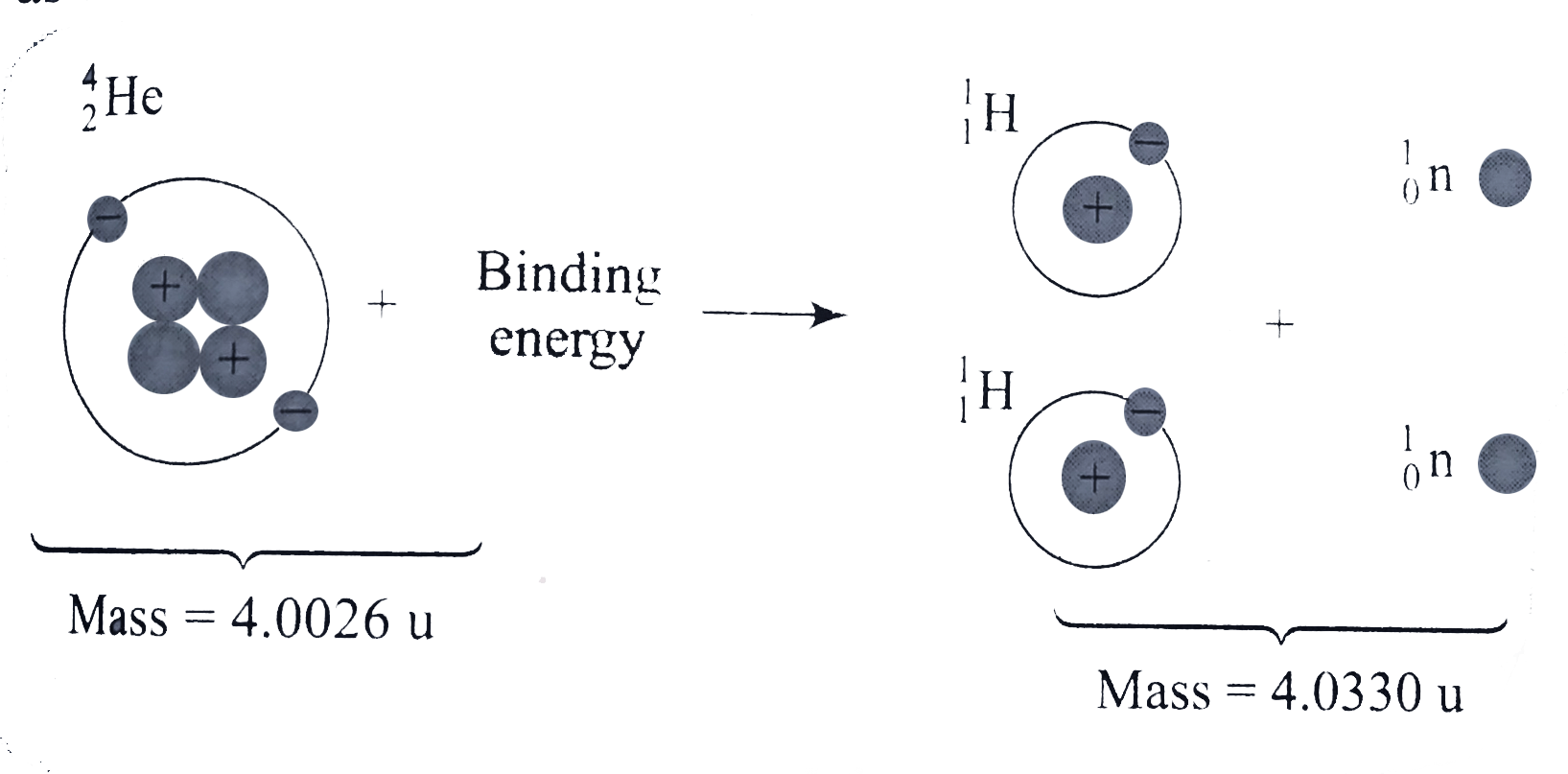
- The atomic mass . 2^4He is 4.0026 u and the atomic mass of .1^1H is ...
Text Solution
|
- An antomic Power station has a generating capacity of 200 MW. The ener...
Text Solution
|
- 200 MeV of energy may be obtained per fission of U^235. A reactor is g...
Text Solution
|
- If 200 MeV energy is released in the fission of a single U^235 nucleus...
Text Solution
|
- Energy released in the fission of a single .92 U^235 nucleus is 200 Me...
Text Solution
|
- If a proton and anti-proton come close to each other and annihilate, h...
Text Solution
|
- Energy released in fusion of 1 kg of deuterium nuclei.
Text Solution
|
- If the energy released in the fission of the nucleus is 200 MeV. Then ...
Text Solution
|
- To generate a power of 3.2 mega watt, the number of fissions of U^235 ...
Text Solution
|
- The binding energy per nucleon of deuterium and helium atom is 1.1 MeV...
Text Solution
|
- The energy liberated on complete fission of 1 kg of .92 U^235 is (Assu...
Text Solution
|
- The nuclear reaction .^2H+.^2H rarr .^4 He (mass of deuteron = 2.0141 ...
Text Solution
|
- Fission of nuclei is possible because the binding energy per nuclei in...
Text Solution
|
- An atomic power nuclear reactor can deliver 300 MW. The energy release...
Text Solution
|
- Which of the following statement (s) is//are correct (may have more th...
Text Solution
|
- Match the statements of column I and column II
Text Solution
|