A fixed thermally conducting cylinder has a radius R and height `L_0`. The cylinder is open at the bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is `P_0`.

The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be

Options

A. `((2p_0piR^2)/(piR^2p_0+Mg))(2L)`
B. `((p_0piR^2-Mg)/(piR^2p_0))(2L)`
C. `((p_0piR^2+Mg)/(piR^2p_0))(2L)`
D. `((p_0piR^2)/(piR^2p_0-Mg))(2L)`

Answer

D

Explanation

Let `p` be the pressure in equilibrium, then
`pA=p_(0)A-Mg`

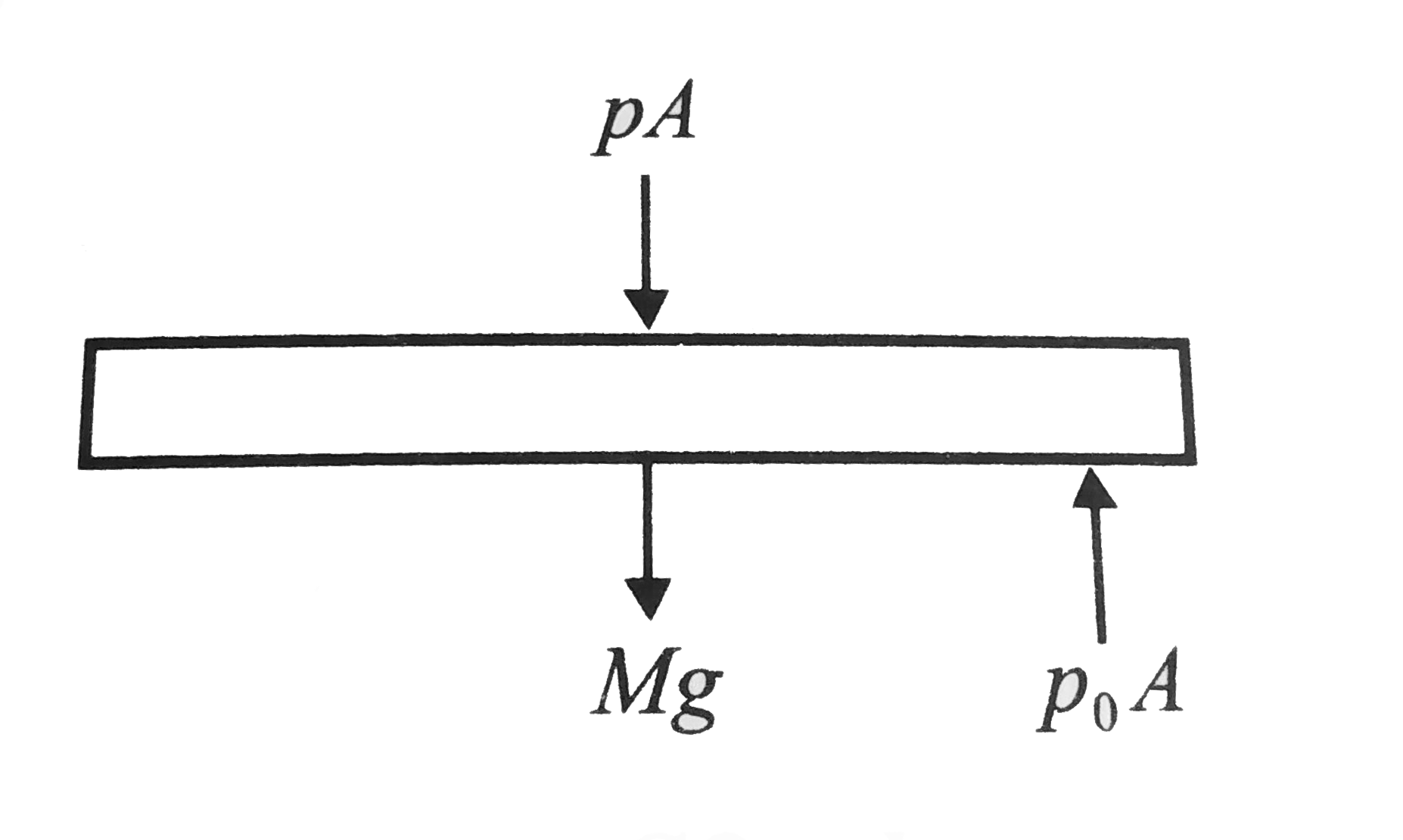
`p=p_(0)-(Mg)/(A)=p_(0)-(Mg)/(piR^(2))`
Applying `p_(1)V_(1)=p_(2)V_(2)`
`L'=(2p_(0)L)/(p)=((p_(0))/(p_(0)-(Mg)/(piR^(2))))(2L)`
`=((p_(0)piR^(2))/(piR^(2)p_(0)-Mg))(2L)`
Therefore, option `(d)` is correct.