Text Solution
Verified by Experts
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Exercise 4.1|23 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Exercise 4.2|23 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Multiple Correct Answer Type|9 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Solved Example
- A uniform horizontal plank is resting symmetrically in a horizontal po...
Text Solution
|
- A uniform plank of mass m, free to move in the horizontal direction o...
Text Solution
|
- A block of mass m hangs by means of a string which goes over a pulley ...
Text Solution
|
- The pulley shown in figure has a moment of inertias I about its xis an...
Text Solution
|
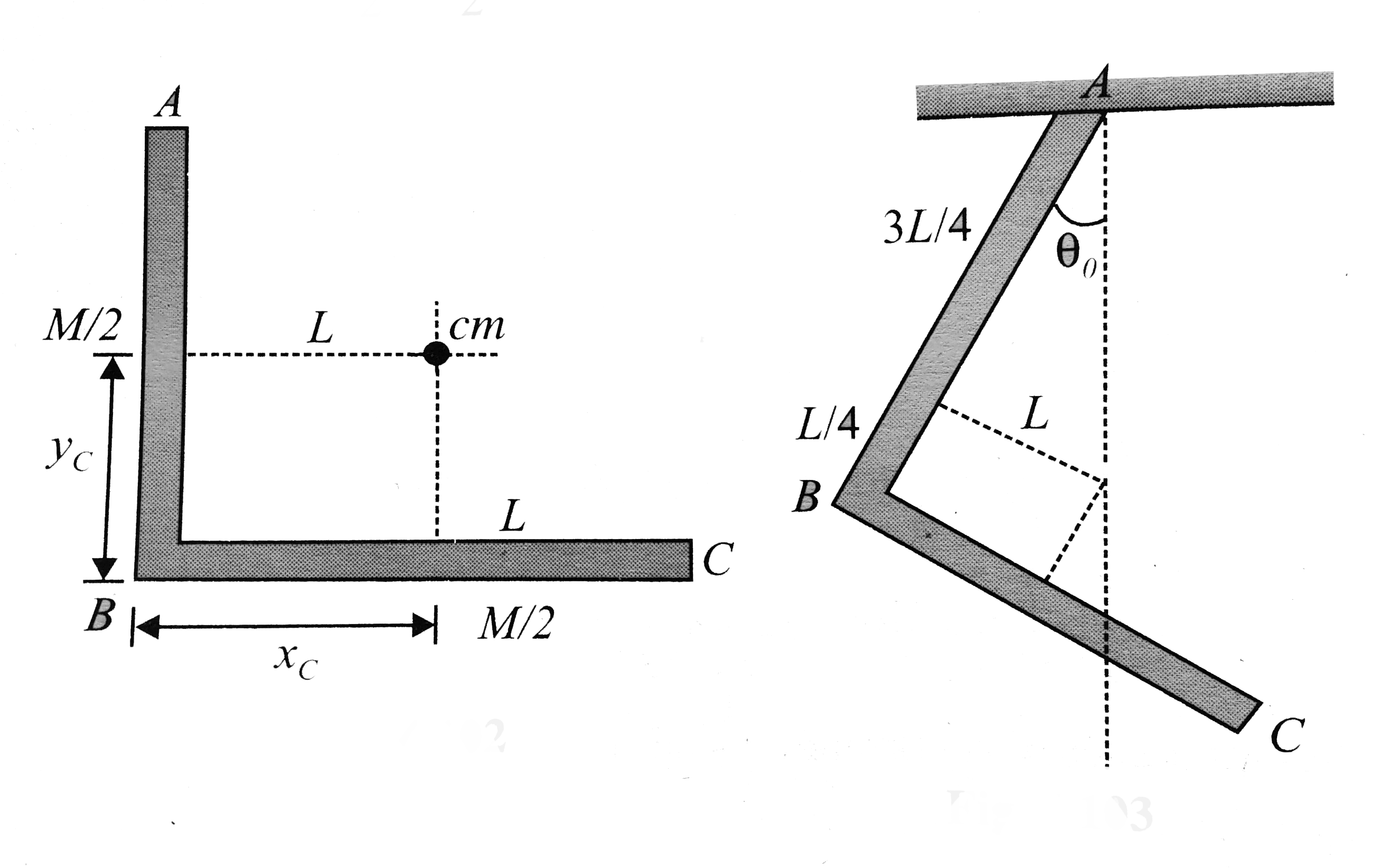
- An L-shaped bar of mass M is pivoted at one of its end so that it can ...
Text Solution
|
- A certain of a perfect gas is enclosed in a cylinder of volume V(0) fi...
Text Solution
|
- A spherical ball of mass m and radius r rolls without slipping on a ro...
Text Solution
|
- A simple pendulum of length L and mass m has a spring of force constan...
Text Solution
|
- One end of an ideal spring is fixed to a wall at origin O and axis of ...
Text Solution
|
- A circular spring of natural length l(0) is cut and weided with two be...
Text Solution
|
- A uniform cylinder of mass m and radius R is in equilibrium on an inc...
Text Solution
|
- A 2kg mass is attached to a spring of force constant 600 N//m and res...
Text Solution
|
- A spring block pendulum is shown in figure . The system is hanging in ...
Text Solution
|
- Figure shown a spring block system hanging in equilibrium. The block o...
Text Solution
|
- Figure shown a block P of mass m resting on a smooth horizontal surfac...
Text Solution
|