Text Solution
Verified by Experts
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Exercise 4.2|23 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Subjective|21 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Solved Example|15 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Exercise 4.1
- Suppose a tunnel is dug along a diameter of the earth. A particle is d...
Text Solution
|
- The equation of motion of a particle started at t=0 is given by x=5sin...
Text Solution
|
- A partical starts SHM frommean position O executing SHM A and B are th...
Text Solution
|
- If the maximum speed and acceleration of a partical executing SHM is 2...
Text Solution
|
- A partical is performing SHM of amplitude 'A' and time period 't'. Fi...
Text Solution
|
- A particle of mass 2 kg is moving of a straight line under the actin f...
Text Solution
|
- A partical executing simple harmonic motion has amplitude of 1 m and t...
Text Solution
|
- In the previous question, find maximum velocity and maximum accelerati...
Text Solution
|
- A partical in SHM ha a period of 4s .It takes time t(1) to start from ...
Text Solution
|
- A particle is subjected to two simple harmonic motion in the same dire...
Text Solution
|
- A particle executes SHM of period 1.2 s and amplitude 8cm. Find the ti...
Text Solution
|
- A cylinder of mass M and radius R is resting on a horizontal platform ...
Text Solution
|
- The figure shows the displacement-time graph of a particle executing S...
Text Solution
|
- A boby excuting SHM has its velocity its 10 cm//see and7 cm//see when ...
Text Solution
|
- A body undergoing SHM about the origin has its equation is given by X=...
Text Solution
|
- The acceleration-displacement (a-X) graph of a particle executing simp...
Text Solution
|
- A block is kept on a horizontal table. The stable is undergoing simple...
Text Solution
|
- A linear harmonic oscillator has a total mechanical energy of 200 J. P...
Text Solution
|
- The potential energy of a particle oscillating along x-axis is given a...
Text Solution
|
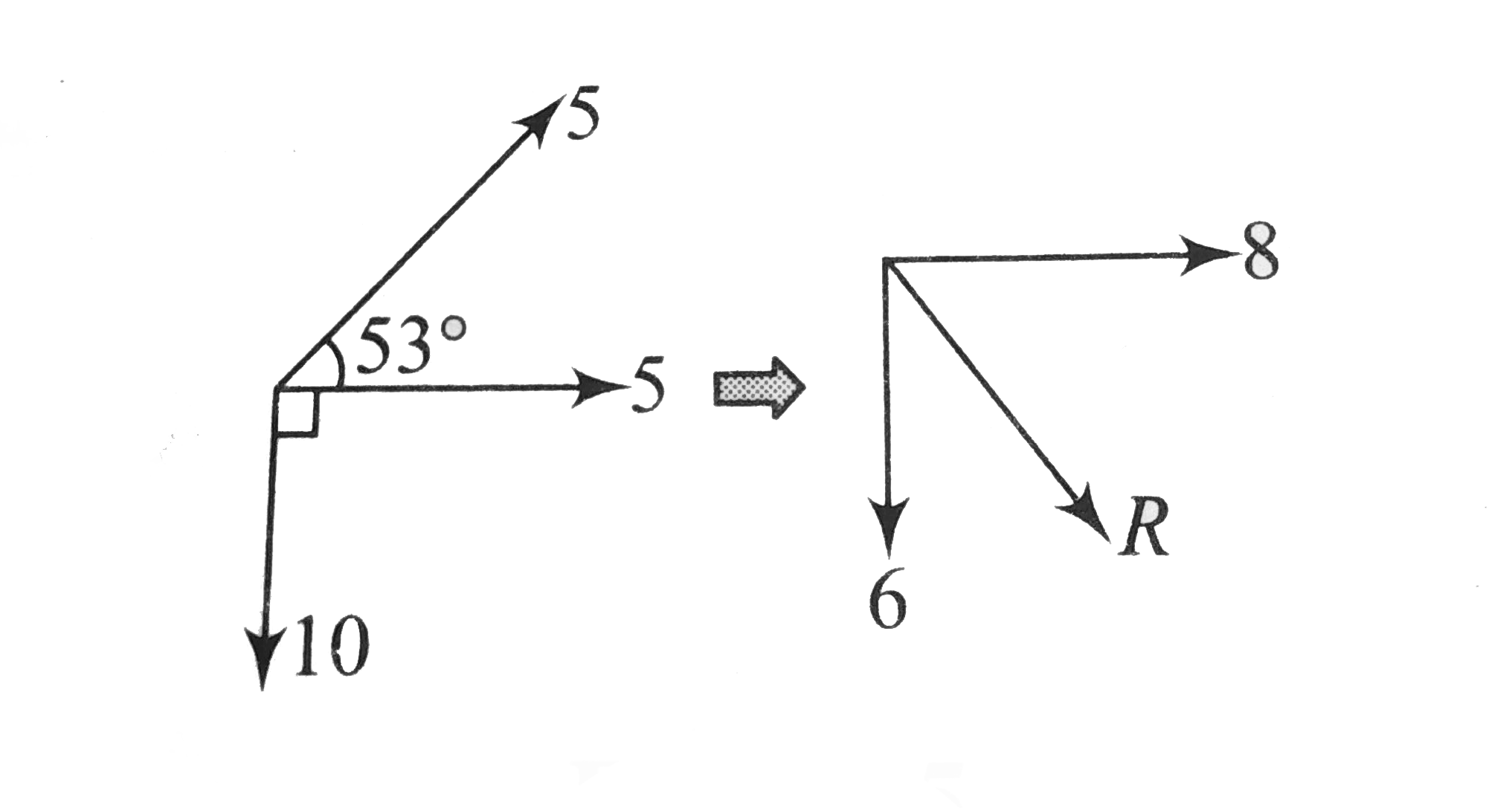
- x(1) = 3 sin omega t x(2) = 5 sin (omega t + 53^(@)) x(3) = -...
Text Solution
|