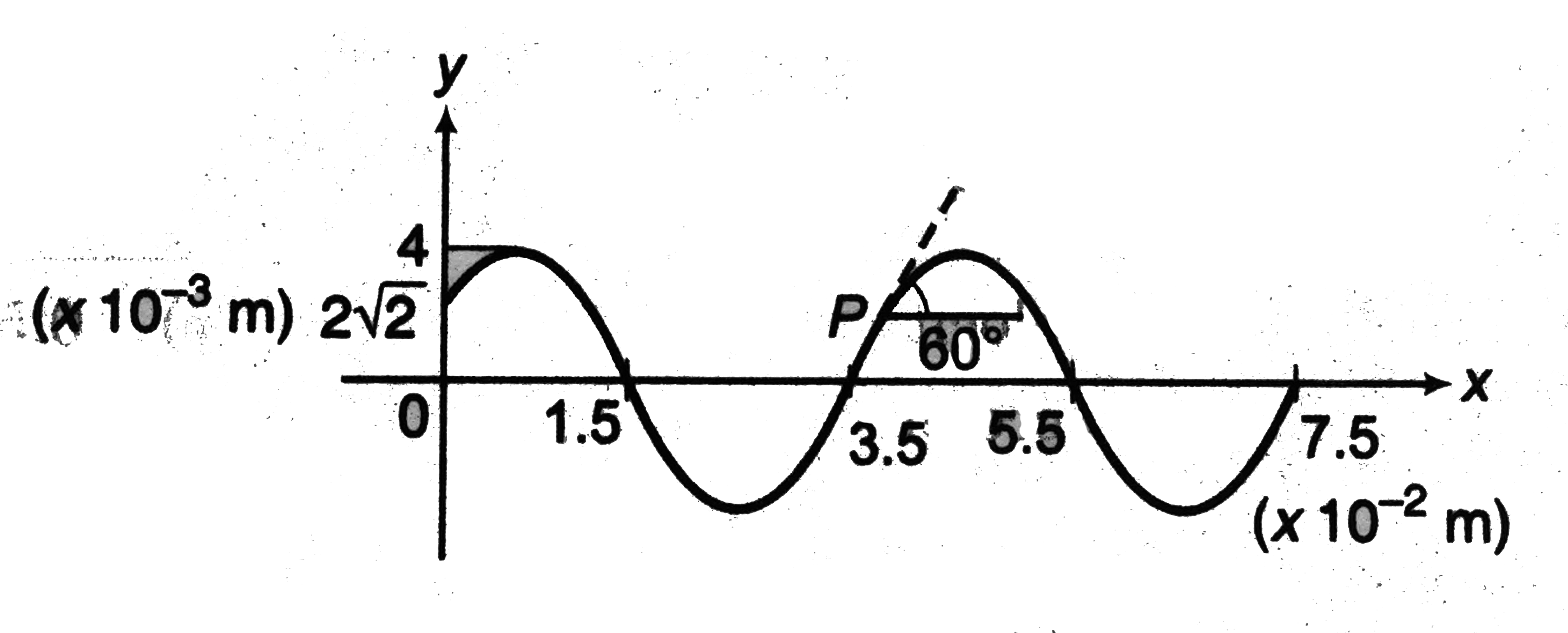
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-TRAVELLING WAVES-Comprehension
- A child playing with a long rope ties one end holds the other. The ro...
Text Solution
|
- A child playing with a long rope ties one end holds the other. The ro...
Text Solution
|
- One end of a long rope is tied to a fixed vertical pole. The rope is s...
Text Solution
|
- One end of a long rope is tied to a fixed vertical pole. The rope is s...
Text Solution
|
- One end of a long rope is tied to a fixed vertical pole. The rope is s...
Text Solution
|
- One end of a long rope is tied to a fixed vertical pole. The rope is s...
Text Solution
|
- One end of a long rope is tied to a fixed vertical pole. The rope is s...
Text Solution
|
- A rope is attached at one end to a fixed vertical pole . It is stretch...
Text Solution
|
- A rope is attached at one end to a fixed vertical pole . It is stretch...
Text Solution
|
- A rope is attached at one end to a fixed vertical pole . It is stretch...
Text Solution
|
- A rope is attached at one end to a fixed vertical pole . It is stretch...
Text Solution
|
- A simple harmonic plane wave propagatees along x-axis in a medium. The...
Text Solution
|
- A simple harmonic plane wave propagatees along x-axis in a medium. The...
Text Solution
|
- Figure. shows two snapshots of medium particle supporting a plane prog...
Text Solution
|
- Figure .shows two snapshots of medium particle supporting a plane prog...
Text Solution
|
- The figure shows a snap photograph of a vibrating string at t = 0. The...
Text Solution
|
- The figure shows a snap photograph of a vibrating string at t = 0. The...
Text Solution
|
- A pulse is started at a time t=0 along the +xdirection on a long, taut...
Text Solution
|
- A pulse is started at a time t=0 along the +xdirection on a long, taut...
Text Solution
|
- A pulse is started at a time t=0 along the +xdirection on a long, taut...
Text Solution
|