Home
Class 10
MATHS
In the following figure, seg DH bot seg...

In the following figure,` seg DH bot seg EF and seg GK bot seg EF. If DH = 6 cm, GK = 10 cm and A(Delta DEF) = 150 cm^(2)`, then find :
` i. EF`
` ii. A(Delta GEF) `
` iii. A( square DFGE). `

Promotional Banner

Topper's Solved these Questions

  • GEOMETRY MARCH 2018

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise Attempt any two sub-questions from the following :|6 Videos

  • GEOMETRY MARCH 2018

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise Attempt any four sub-questions from the following :|6 Videos

  • GEOMETRY MARCH 2015

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise Solve any two sub-questions:|11 Videos

  • GEOMETRY MARCH 2019

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise QUESTIONS|20 Videos

Similar Questions

Explore conceptually related problems

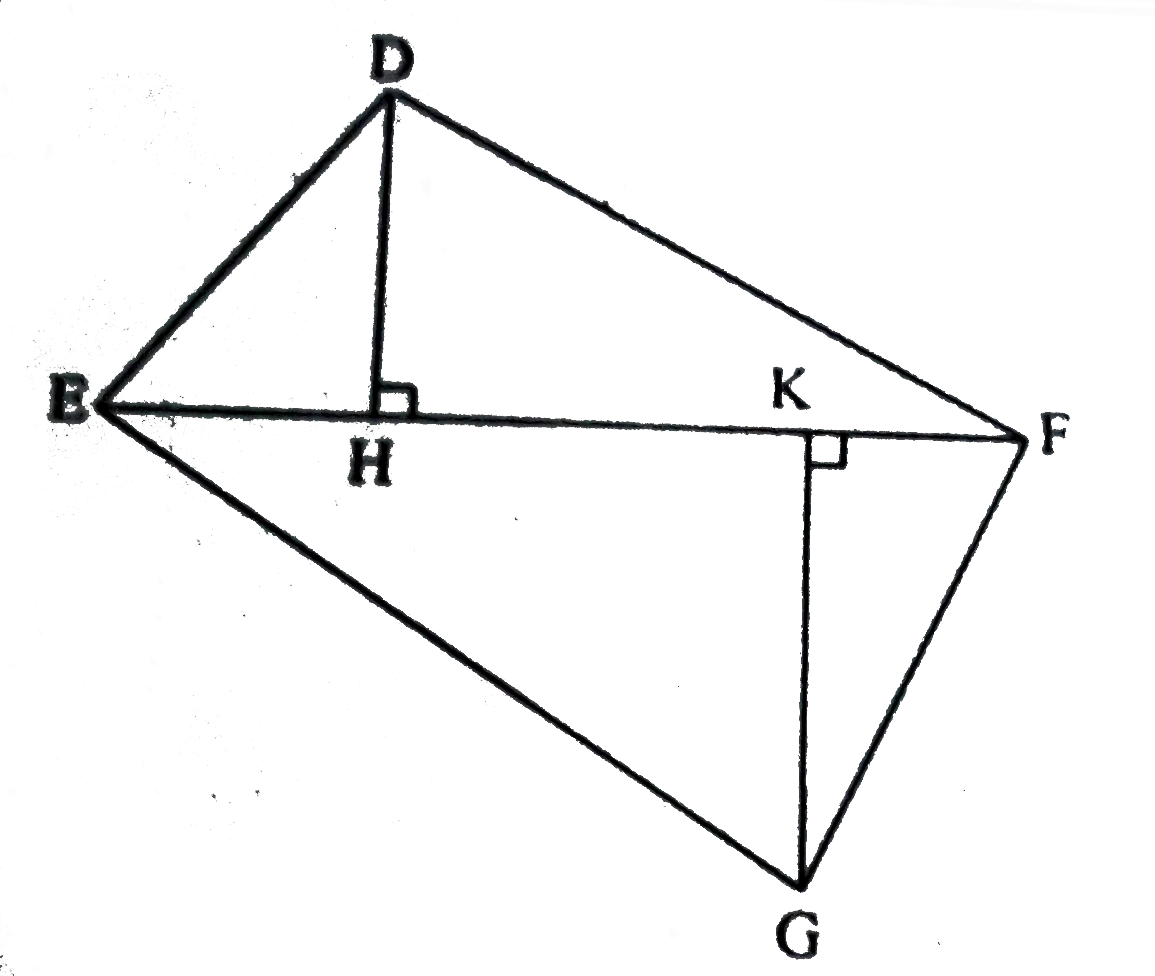
In the following figure, seg DH bot seg EF and seg GK bot EF. If DH = 6 cm, GK = 10 cm and A(DeltaDEF) = 150 cm^2 , then find: (i) EF (ii) A (DeltaGEF) (iii) A(squareDFGE)

In the figure, set DH_|_ side EF and seg GK_|_ side EF. If DH=12cm, GK=20 and A(DeltaDEF)=300cm^(2) . Find (i) EF(ii) A(DeltaGEF) (iii) A(squareDEGF) .

In the given figure, seg BE bot seg AB and seg BA bot seg AD. If BE = 6 and AD = 9, then find (A(DeltaABE))/(A(DeltaBAD)) .

DeltaABC ~ DeltaDEF . If BC = 5 cm,EF = 7.5 cm and A(Delta DEF) = 45cm^2 , then A(DeltaABC) =

In given figure, seg AE bot seg BC, seg DF bot line BC, AE = 4, DF = 6, then find (A(DeltaABC))/(A(DeltaDBC)) .

In the following figure AB||CD||EF||GH and BH=100 cm. find x and y.

In the adjoining figure, seg EF abs() side AC, AB = 18, AE = 10, BF = 4. Find BC.

In the figure, seg AB|| seg CD|| seg EF AC=1.5 , BD=10 , DF=6 then AE=?

(A) Complete any two out of three activites : In the figure , seg SP bot side YK . Seg YT bot side SK . If SP = 6 , YK = 13, YT = 5 and TK = 12 then complete the following activity to find A (Delta SYK ) : A (Delta YTK) The ratio of the areas of the two Deltas is equal to the ratio of the products of their square and the corresponding heights :. (A(Delta SYK))/(A (Delta YTK)) = (square xxSP)/(TK xx TY) = (13 xx 6) /(12 xx square ) = square /square

If Delta ABC is similar to Delta DEF such that BC = 3 cm, EF = 4 cm and area of Delta ABC = 54 cm^(2) , then the area of Delta DEF is :