Home
Class 12
PHYSICS
A batsman hits a sixes and the ball touc...

A batsman hits a sixes and the ball touches the ground outside the cricket ground. Which of the following graph describes the variation of the cricket ball's vertical velocity v with time between the time `t_1` as it hits the bat and time `t_2` when it touches the ground?

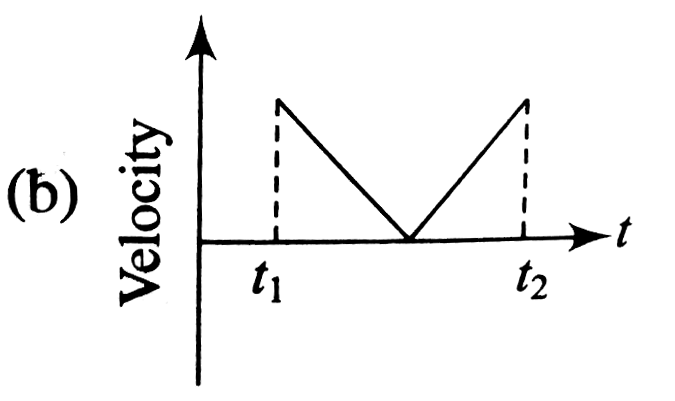
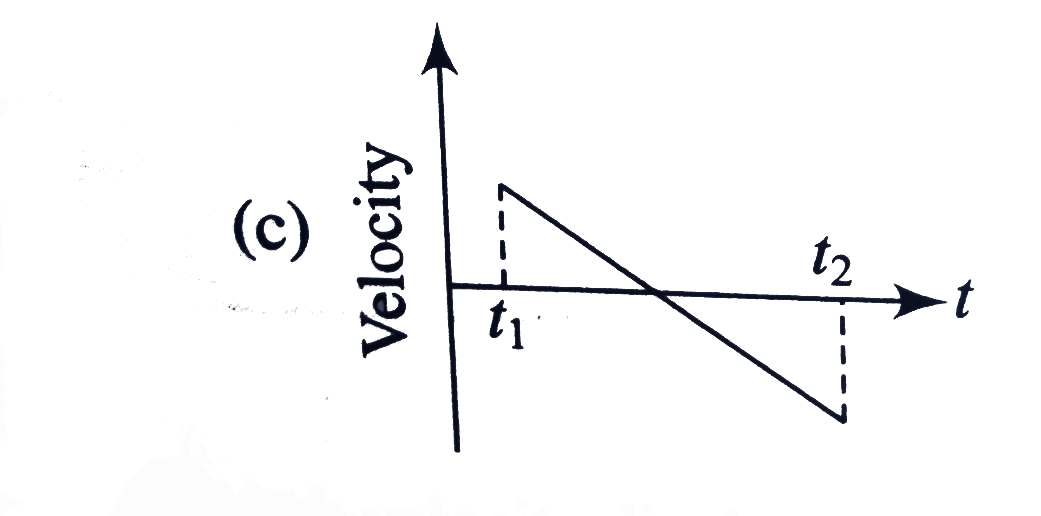
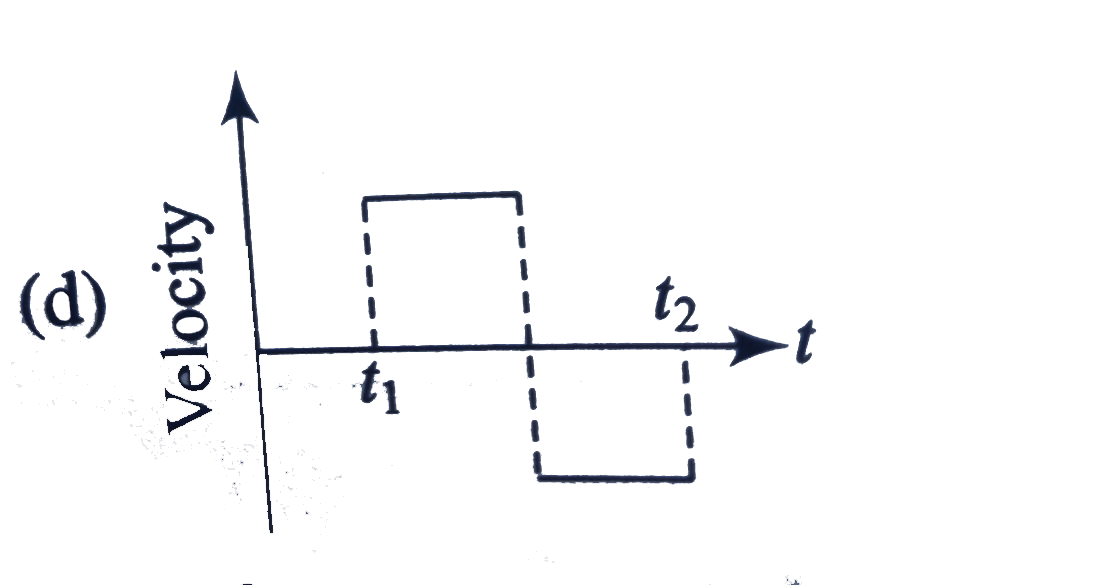
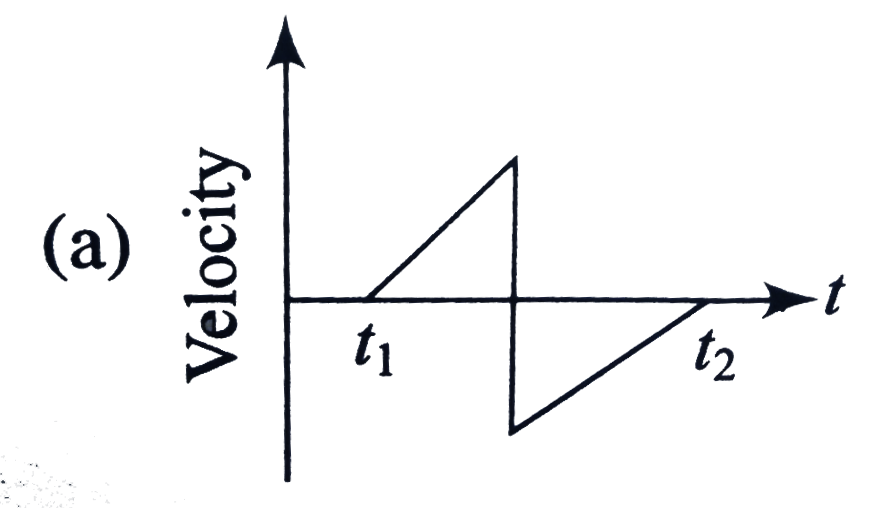A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
At time `t_1` the velocity of ball will be maximum andit goes on decreasing with respect to time.
At the highest point of path its velocity becomes zero, then it increases but direction is reversed
This explanation match with graph (c ).
Promotional Banner

Similar Questions

Explore conceptually related problems

The graph shown the variation with times t of the velocity v of an object . Which one of the following graphs best represents the variation of acceleration a of the object with time t ?

Which of the following is the graph between the height (h) of a projectile and time (t), when it is projected from the ground

A batsman hits a cricket ball which then rolls on a level ground . After covering a short distance, the ball comes to rest, The ball slows to a stop because

A particle is projected vertically upwards with a velocity v. It returns to the ground in time T. Which of the following graphs correctly represents the motion.

A particle is thrown vertically upwards with a velocity v . It returns to the ground in time T. which of the following graphs correctly represents the motion ?

Which of the following change appreciably when a batsman hits a moving cricket ball ? A. Shape B. Direction C. Size D. speed

A ball falls from a height ‘h’ and collides with the ground. Each time it collides, its velocity is halved. Which of the following graphs are correct? Here t, v and y represent time, velocity and height above ground respectively. (vertically upwards direction is taken as positive and ground as y = 0)

A ball is thrown vertically upward with a velocity u from the top of a tower. If it strikes the ground with velocity 3u, the time taken by the ball to reach the ground is