Home
Class 12
PHYSICS
A particle is projected from point A on ...


A particle is projected from point A on plane AB, so that `AB=(2u^2tantheta)/(gsqrt3)` in the figure as shown. If u is the velocity of projection, find angle `theta`.

A

`30^@`

B

`60^@`

C

`90^@`

D

`45^@`

Text Solution

Verified by Experts

The correct Answer is:
A
Time of flight `t=(2u sin (2theta-theta))/(g cos theta)=(2u)/(g)tantheta`
`AB=(2u^(2)tantheta)/(gsqrt(3))=(u)/(sqrt3)t` ..(i)
`u_H=ucos2theta`
`AC=u_H.t=ucos2thetat`
`AB=(AC)/(costheta)=(ucos2thetat)/(costheta)` …(ii)
Compare equations (i) and (ii)
`(cos2theta)/(costheta)=(1)/(sqrt3)` or `theta=30^@`
Promotional Banner

Similar Questions

Explore conceptually related problems

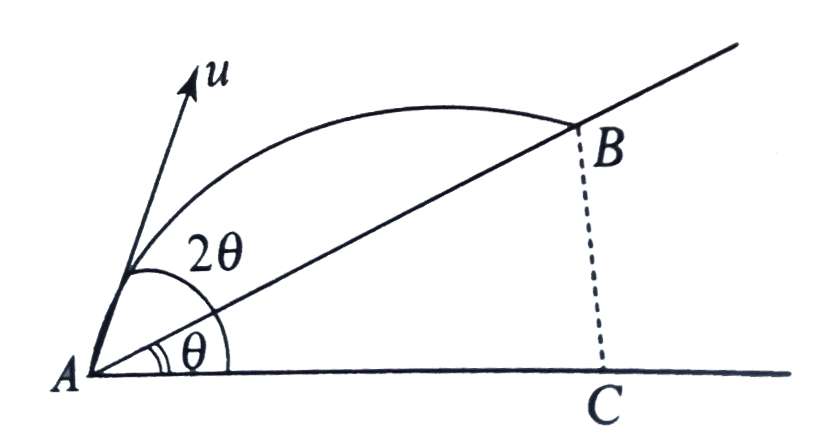
A particle is projected horizontally with a speed u from the top of plane inclined at an angle theta with the horizontal. How far from the point of projection will the particle strike the plane ?

A particle is projected horizontal with a speed u from the top of plane inclined at an angle theta with the horizontal. How far from the point of projection will the particle strike the plane?

Figure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle alpha with vertical. The particles collide at point Q on the plane. Then

A particle is projected from a point on the level ground and its height is h when at horizontal distances a and 2 a from its point of projection. Find the velocity of projection.

A particle is projected at point A from an inclination plane with inclination angle theta as shown in figure. The magnitude of projection velocity is vecu and its direction is perpendicular to the plane. After some time it passes from point B which is in the same horizontal level of A, with velocity vecv . Then the angle between vecu and vecv will be

A particle is projected with initial speed u at an angle theta above the horizontal . Let A be the point of projection , B the point where velocity makes an angle theta //2 above the horizontal and C the highest point of the trajectory . Radius of curvature of the trajectory at point A is

A particle is projected with initial speed u at an angle theta above the horizontal . Let A be the point of projection , B the point where velocity makes an angle theta //2 above the horizontal and C the highest point of the trajectory . Radius of curvature of the trajectory at point C is

A particle is projected with initial speed u at an angle theta above the horizontal . Let A be the point of projection , B the point where velocity makes an angle theta //2 above the horizontal and C the highest point of the trajectory . Radius of curvature of the trajectory at point B is

A particle is projected from the top of a tower of height H. Initial velocity of projection is u at an angle theta above the horizontal . Particle hits the ground at a distance R from the bottom of tower. What should be the angle of projection theta so that R is maximum ? What is the maximum value of R?

What is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle theta with the horizontal, at a point where the velocity of particle makes an angle theta//2 with the horizontal.