Home
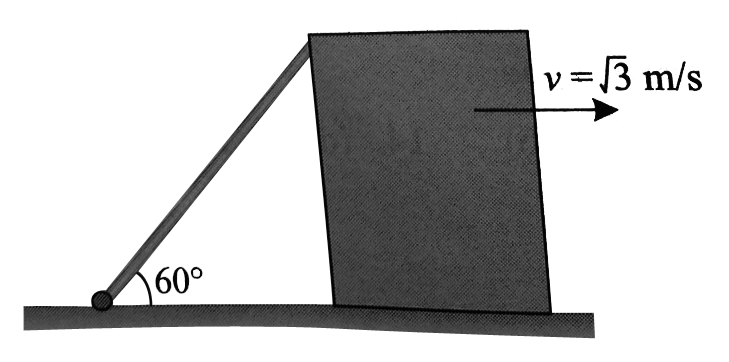
Class 12
PHYSICS
A rod AB is shown in figure. End A of th...


A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity m/s towards right. The velocity of end B of rod when rod makes an angle of `60^@` with ground is :

A

`sqrt(3)(m)/(s)`

B

`2(m)/(s)`

C

`2sqrt(3)(m)/(s)`

D

`3(m)/(s)`

Text Solution

Verified by Experts

The correct Answer is:
B
Let `AB=l`,`B=(x,y)`
`vecv_B=v_xhati+v_yhatj`
`vecv_B=sqrt(3)hati+v_yhatj`
`x^2+y^2=l^2`
`2xv_x=2yv_y=0`
`impliessqrt(3)+(y)/(x)v_y=0`
`impliessqrt(3)+(tan60^@)v_y=0`
Hence from 9i)
`vecv_B=sqrt(3)hati-hatj`
Hence `v_b=2(m)/(s)`
Promotional Banner

Similar Questions

Explore conceptually related problems

A rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2 ms^-1 towards right. The velocity of end B of rod at the instant shown in figure is

A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Vertical component of the force applied by the hinge

A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Horizontal component of the force applied by the hinge

Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle theta with the horizontal.

A rod of length l whose lower end is fixed on a horizontal plane, starts toppling from the vertical position. The velocity of the upper end when it hits the ground is.

In the figure shown the end A of the rod of length L is being pushed down parallel to the inclined surface with a velocity =v let the velocity of end B=u and the angular velocity of the rod = omega then

Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle theta with the horizontal.

End A of a rod AB is being pulled on the floor with a constant velocity v_(0) as shown. Taking the length of the rod as l , at an instant when the rod makes an angle 37^@ with the horizontal, calculate the velocity of the CM of the rod