A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two blocks, of masses M and 2 M, are connected to a light spring of sp...
Text Solution
|
- A block of mass 2.0 kg is moving on a frictionless horizontal surface ...
Text Solution
|
- A block of mass m held touching the upper end of a light spring of for...
Text Solution
|
- In the figure shown a block of masss m is atteched at ends of two spri...
Text Solution
|
- Two spring are connected toa block of mass M placed a frictionless sur...
Text Solution
|
- Two blocks, of masses M and 2 M , are connected to a light spring of s...
Text Solution
|
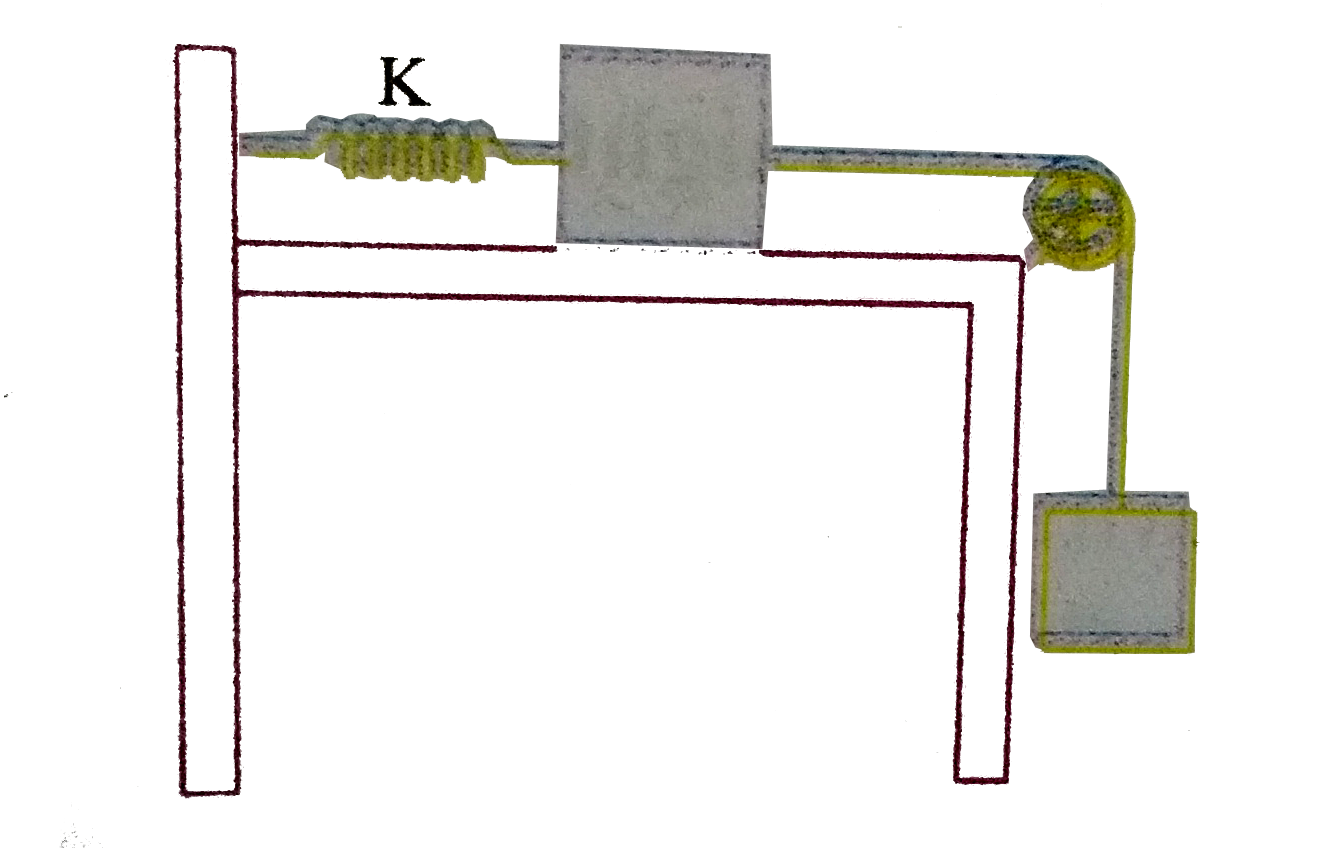
- An arrangement of spring , strings, pulley and masses is shown in the ...
Text Solution
|
- Two blocks of masses m and m' are connected by a light spring on a hor...
Text Solution
|
- चित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके ए...
Text Solution
|
 .
.