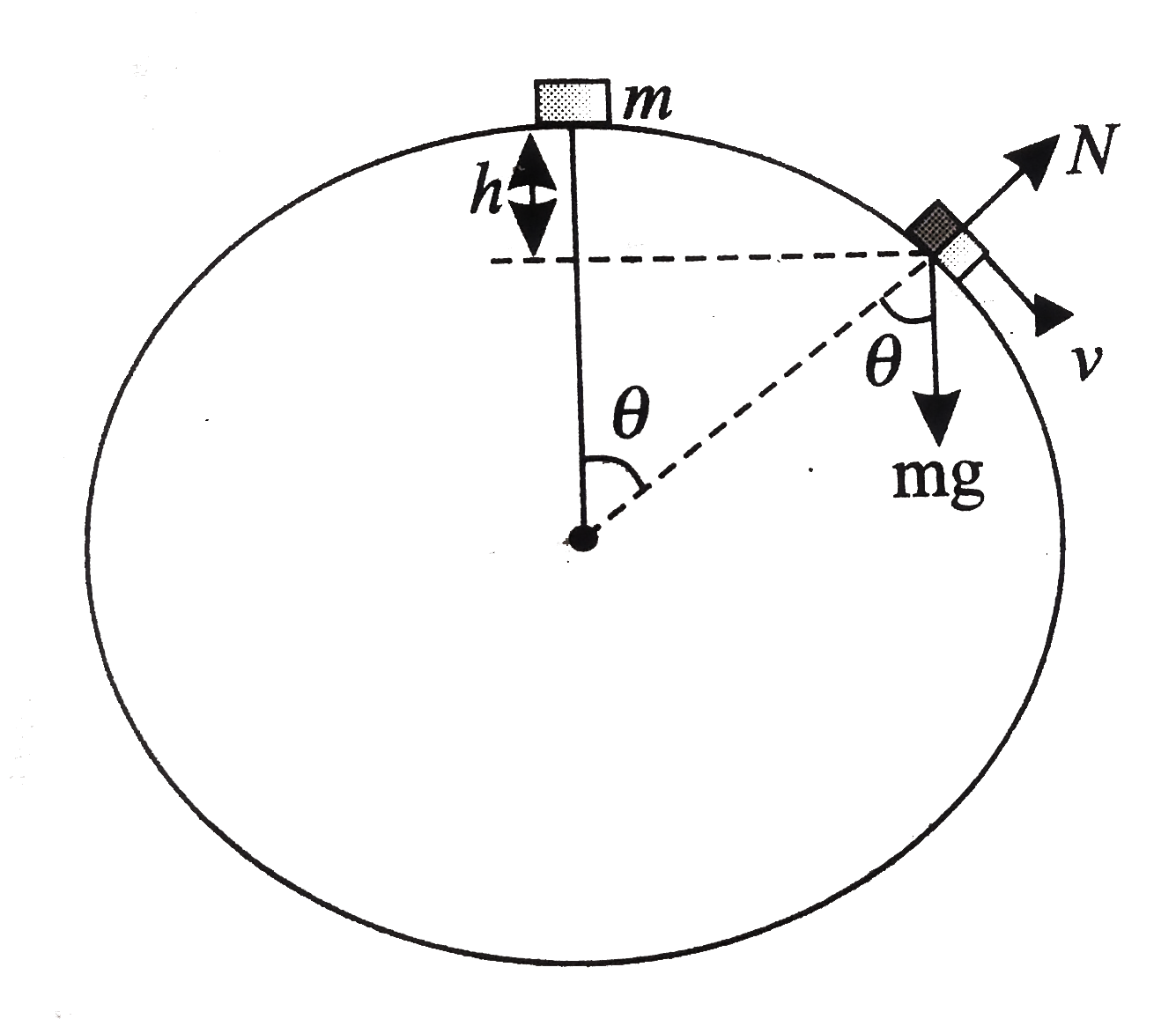
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle originally at rest at the highest point of a smooth vertica...
Text Solution
|
- A partical originally at rest at the highest point of a smooth vertica...
Text Solution
|
- A particle is projected along the inner surface of a smooth vertical c...
Text Solution
|
- A particle of mass m is being circulated on a vertical circle of radiu...
Text Solution
|
- डोरी से बाँधा एक कण r त्रिज्या के उर्ध्वाधर वृत्त में गति कर रहा है। ...
Text Solution
|
- In a vertical circle the minimum or critical velocity at highest point...
Text Solution
|
- एक कण प्रारम्भ में त्रिज्या r के ऊर्ध्वाधर वृत्त उच्चतम बिंदु पर विराम...
Text Solution
|
- ऊर्ध्वाधर वृत्त में गति के वृत्त के निम्नतम बिंदु तथा वृत्त के उच्चतम ...
Text Solution
|
- m द्रव्यमान का एक कण r त्रिज्या के ऊर्ध्वाधर वृत्त में गतिमान है | उच्...
Text Solution
|