A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
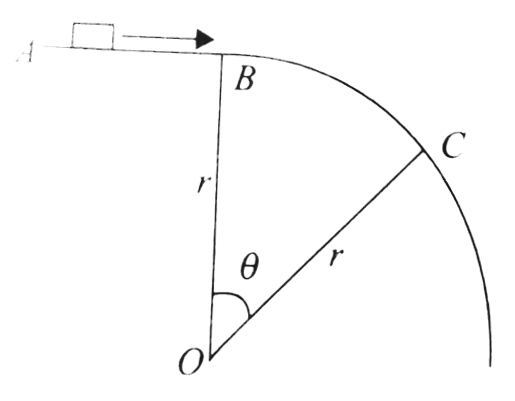
- A small block slides with velocity v0=0.5sqrt(gr) on the horizontal fr...
Text Solution
|
- A small block slides with velocity 0.5sqrt(gr) on the horizontal frict...
Text Solution
|
- A small block slides with velocity v0=0.5sqrt(gr) on the horizontal fr...
Text Solution
|
- In the arrangement shown in the fig, end A of the string is being pull...
Text Solution
|
- In the Fig. the blocks 'A' and 'B' are connected with an inextensible ...
Text Solution
|
- m द्रव्यमान का एक गुटका M द्रव्यमान के एक त्रिभुजाकार गुटक पर रखा हुआ ...
Text Solution
|
- A block of mass m slides down along the surface of the bowl from the r...
Text Solution
|
- A block kept on a rough surface starts sliding when the inclination of...
Text Solution
|
- A block kept on a rough surface starts sliding when the inclination of...
Text Solution
|