Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL AND CAPACITANCE
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Very Short Answer Questions|10 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Short Answer Questions|5 VideosELECTROMAGNETIC WAVE
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise ADDITIONAL EXERCISES|19 VideosMAGNETISM AND MATTER
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Additional Exercises|19 Videos
Similar Questions
Explore conceptually related problems
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-ELECTROSTATIC POTENTIAL AND CAPACITANCE-SAQs
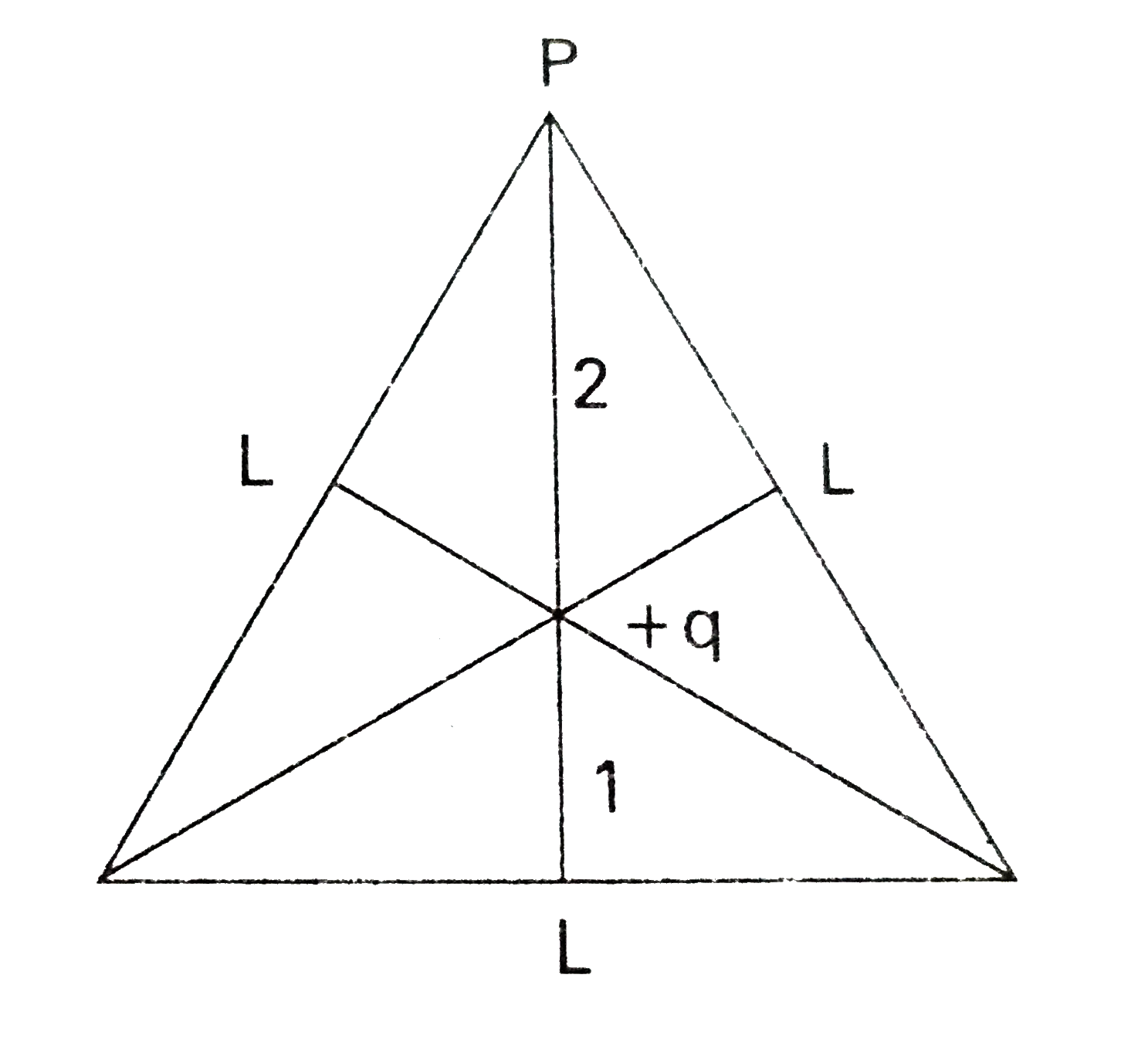
- An equilateral triangle has a side length L. A charge +q is kept at th...
Text Solution
|
- What is series combination of capacitors. Derive the formula for equiv...
Text Solution
|
- What is parallel combination of capacitors. Derive the formula for equ...
Text Solution
|
- Derive an expression for the energy stored in a capacitor.
Text Solution
|
- What is the energy stored when the space between the plates is filled ...
Text Solution
|