Similar Questions
Explore conceptually related problems
Recommended Questions
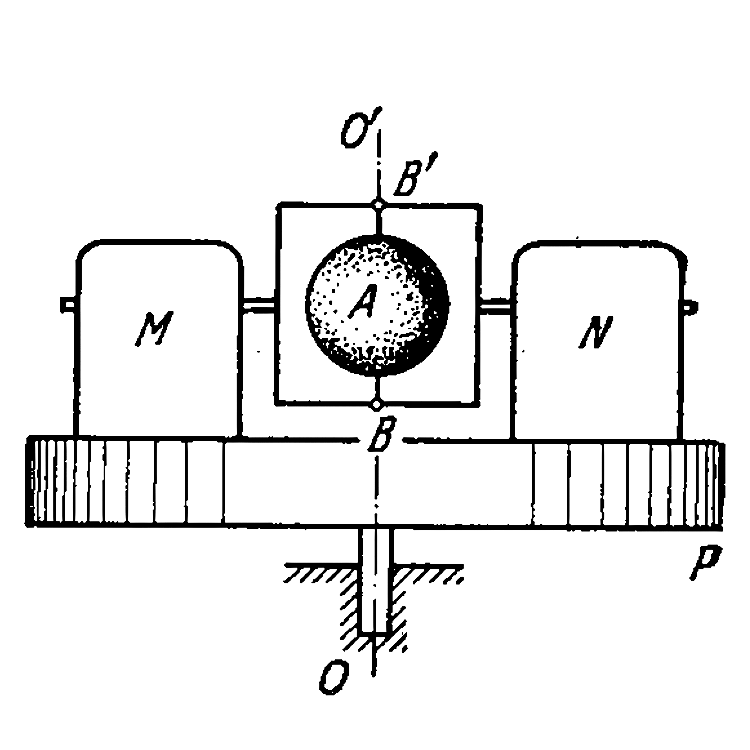
- A stationary platform P which can rotate freely about a vertical axis ...
Text Solution
|
- A uniform of mass m and length L is tied to a vertical shaft. It rotat...
Text Solution
|
- A man of mass m stands on a horizontal platform in the shape of a disc...
Text Solution
|
- A child of mass m is standing, on the periphery of a circular platform...
Text Solution
|
- A stationary platform P which can rotate freely about a vertical axis ...
Text Solution
|
- एक जड़त्वीय फ्रेम में एक नियत ऊर्ध्वाधर अक्ष के परितः एक वस्तु एकसमान क...
Text Solution
|
- The moment of an inertia about an axis of a body which is rotating wit...
Text Solution
|
- एक वृत्ताकार प्लेटफॉर्म क्षैतिज तल में अपने केंद्र से जाने वाली ऊर्ध्व...
Text Solution
|
- A smooth rod of length l rotates freely in a horizontal plane with the...
Text Solution
|